Securing Cryptographic Protocols Against Quantum Computers

Posted by ekr on 06 Aug 2021

The security of the Internet depends critically on cryptography. Whenever you log into Facebook or Gmail or buy something on Amazon, you're counting on cryptography to protect you and your data. Unfortunately for cryptography, there's currently a lot of work on developing quantum computers, which have the potential to break a lot of the cryptographic algorithms that we use to secure our data. It's far from clear if and when there will ever be workable quantum computers (see this talk by cryptographer Kenny Paterson, see slides and also here for background), but if one does get built, the Internet as we know it is in big trouble.

A (Very) Brief Overview of Quantum Computing and Cryptography #

In this section, I try to give the very barest overview of what you need to know about quantum computing and its impact on cryptography. This will really be inadequate for any real understanding, but rather is just what you need to know to follow the rest of this post.

The first thing to know is that the security of real-world cryptographic algorithms depends on computational complexity. For example, a typical "symmetric" encryption algorithm such as the Advanced Encryption Standard (AES) uses a key to encrypt data. The number of possible keys is very large (2¹²⁸ for typical uses of AES) but not infinite, so in principle you could just try to decrypt the encrypted data with every key in sequence until you get a result that looks sensible.^[1] This is called "exhaustive search" or sometimes "brute force". However, 2¹²⁸ is a very big number and it is not practical to try all those keys with any normal computer, even of unreasonable size.^[2]

Quantum computers use quantum mechanical techniques to speed up this process. One way to get some intuition for this is to think of it like quantum computers let you try a lot of different keys at once (think superposition and Schrodinger's Cat) and only get the answer for the one that was right. The result is that a sufficiently powerful quantum computer can do some computations in practical time -- like breaking an encryption algorithm -- that would otherwise not be practical. This creates a problem for us in the real-world. There are some very difficult engineering problems in building a large quantum computer, but we also don't know that they are insurmountable.

Quantum Computers and Communications Security Protocols #

Like quantum computing, the design of communications security protocols is also a very complicated topic, but again here is the barest overview of what you need to follow along.^[3] If we look at a typical channel security protocol like TLS, we can see that there are three major cryptographic functions being performed:

• Key Establishment. The peers negotiate a cryptographic key which they can use to encrypt data. This key is authenticated in the next step.

• Authentication. The peers authenticate to each other. In the case of TLS, this usually means that the server (e.g., Amazon) proves its identity to the client (i.e., you).

• Bulk Encryption. The peers use the key established in the previous step to actually protect (encrypt and authenticate) the data they want to send (e.g., your credit card number). All this data is tied back to the previous authentication step because only the right peer will have the key.

The reason for this structure is that authentication and key establishment usually make use of what's called "asymmetric" or "public key" algorithms, which allow two people who don't share a secret to communicate.^[4]These algorithms are powerful but slow. Once you have established a key, you then use "symmetric" algorithms to actually protect the data. These algorithms are much faster but require you to already share a key. Most encryption systems, whether e-mail, voice encryption, or instant messaging share this basic structure, though for non-interactive use cases like e-mail, with everything bundled into a single message. Systems that just provide authenticity (e.g., certificates) obviously don't have key establishment or bulk encryption.

This brings us to quantum computers. The best known quantum computing algorithms weaken (see: Grover's Algorithm) the standard symmetric algorithms, which means that you can protect yourself -- or so it seems -- by doubling the key size, which is practical. However, they completely break (see: Shor's Algorithm) all the standard asymmetric algorithms, more or less at any key size. If the asymmetric algorithms are broken, then the attacker can just recover the key you are using and decrypt your traffic (or impersonate the peer) without attacking the symmetric algorithm at all, which is obviously catastrophic. In other words, we need some new asymmetric algorithms which are secure even against quantum computers.^[5]

Post-Quantum Algorithms for Protocols #

The good news is that there are new "post-quantum" (PQ) cryptographic algorithms (the current algorithms are usually called classical algorithms by analogy to classical mechanics). which are not currently known to be breakable with existing quantum algorithms.^[6] Since 2017 NIST has been running a competition to select a set of post-quantum algorithms, with a target of picking something in the 2023-ish time frame. The bad news is that the algorithms are, well, not that great: typically they either are slower, involve sending/receiving more data, or both.^[7] Anyway, people have been looking at how to integrate these new algorithms with existing protocols, though mostly in preparation for when NIST finally declares a winner, which finally brings me to the point of this post, which is how one does that.

Bulk Encryption #

Obviously, the first thing you want to do is to double the key size of your symmetric algorithms. That doesn't require any fancy new crypto, but you still need to do it. Once that's done, the situation gets a bit more complicated.

Key Establishment #

In order of priority the next thing to do is to address key establishment. The reason for this is that even if a quantum computer doesn't exist today an attacker can record all of your traffic in the hope that eventually a quantum computer will exist and they'll be able to decrypt it. Thus, it's helpful to use post-quantum key establishment now.

Instead of just swapping existing key establishment mechanisms for PQ mechanisms, what's actually being proposed is to use them together in what's called a "hybrid" mode. This just means that you do both regular and PQ key establishment and parallel and then mix the results together. This obviously has worse performance than doing either alone but the truth is that people aren't really that confident about the security of PQ algorithms and so this allows you to get a measure of security against quantum computers without worrying that the PQ algorithm will get broken: even if that happens you'll still have as much security as you have now.

This process is farthest along in TLS, where this kind of thing drops in very easily and there have been several trials of hybrid algorithms.^[8] The results are fairly positive: some algorithms have fairly comparable performance to existing public key algorithms, as shown in the graphs below:^[9]

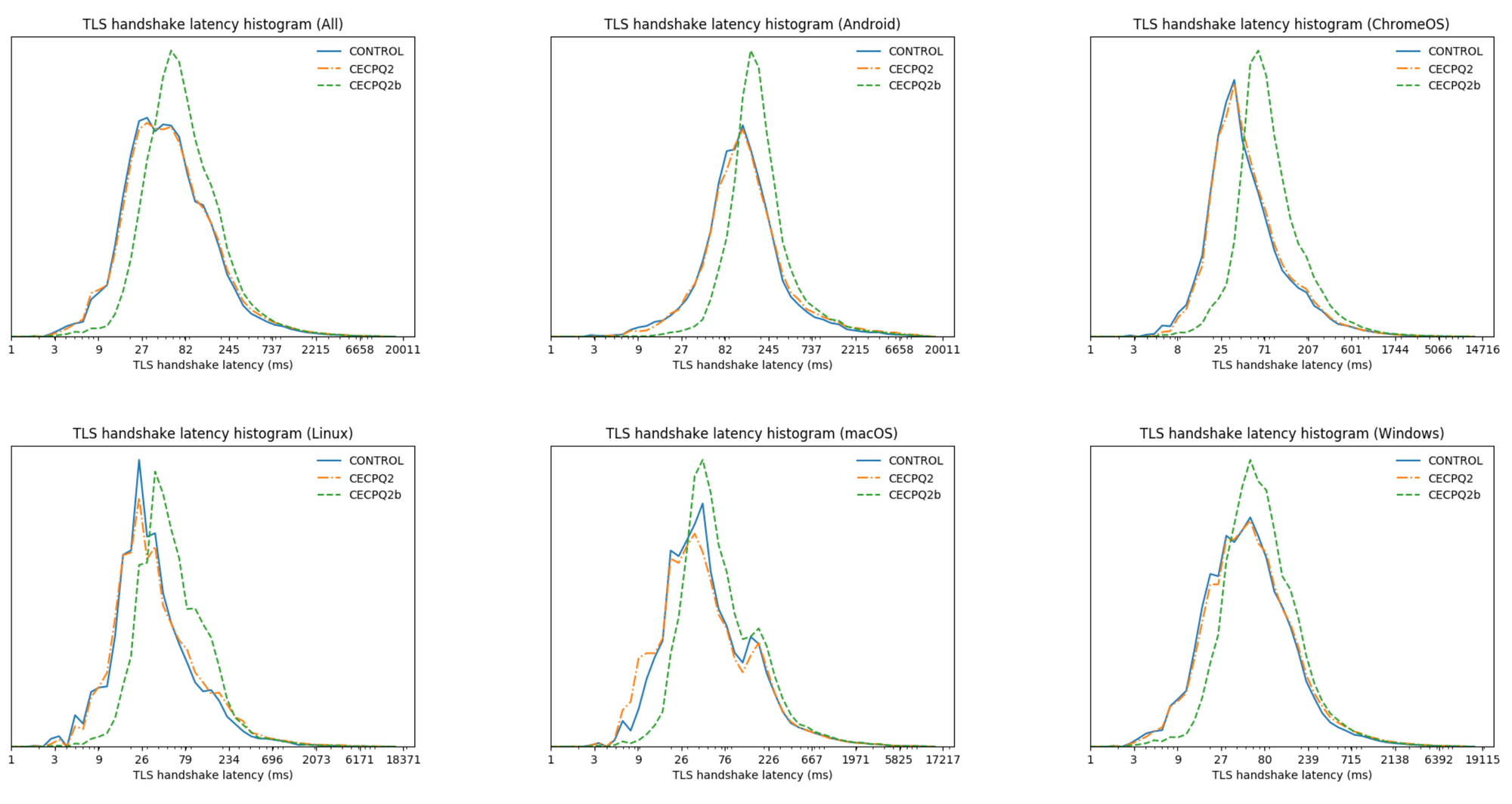
Other channel security protocols like TLS (SSH, IPsec, etc.) should be fairly easy to adapt in similar ways, as should secure e-mail protocols like PGP, S/MIME, etc. The situation for instant messaging applications is a bit more complicated because the PQ algorithms aren't complete drop-in replacements for the existing algorithms (in particular, they mostly don't look exactly like Diffie-Hellman), so it has to be taken on a case-by case basis.

Authentication #

Finally, we need to address authentication. This is lower priority because for a quantum computer to be useful for attacking authentication, the attacker needs to have it before the relying party verifies that authentication. For instance, if we are authenticating a TLS connection then we are primarily concerned with an attacker who is able to impersonate the peer at the time the association is set up. As an example, imagine you are making a TLS connection to Amazon, then the attacker has to already have a quantum computer so that it can break Amazon's key. If it breaks Amazon's key a week later, that doesn't allow it go back in time to impersonate Amazon to you.^[10]

That doesn't mean that post-quantum authentication isn't important: it's going to take a very long time to roll out and so if a quantum computer is developed we're going to want to have all the post-quantum credentials pretty much ready to go. Actually doing this turns out to be a little complicated because you need to operate both classical and post-quantum, algorithms in parallel. To go back to our TLS example, suppose a server gets a post-quantum certificate (for the sake of this discussion, assume it's both signed with a post-quantum algorithm and contains a post-quantum key, because analyzing the mixed case is more difficult). Not every browser will accept PQ algorithms, so servers will also need to have a classical certificate, probably for years to come.^[11] Then when a client connects to the server, they negotiate algorithms and the server provides the appropriate certificate. For non-interactive situations like e-mail, the sender will want to sign with both certificates in parallel.^[12]

It's important to recognize that in many cases it doesn't actually improve the authenticating party's security to have a PQ certificate. The reason is that if the relying party is willing to accept a broken classical algorithm then the attacker can use their quantum computer to forge a classical certificate (or, if the authenticating party has a certificate with a classical algorithm, forge a signature on the certificate) and impersonate the authenticating party directly. In order to have protection against a quantum computer, you need relying parties to refuse to accept the (now) broken algorithms.^[13] This means that authenticating parties (e.g., TLS servers) don't have a huge incentive to roll out PQ certificates quickly.^[14]

The main reason to do so is to enable a quick switch to PQ algorithms if a quantum computer gets built and then clients rapidly move to deprecate classical algorithms; even then, you just need to to be ready to switch quickly enough that the clients won't get ahead of you (or be big enough that they can't afford to). It's not clear to me how much that's going happen here: because the PQ authentication algorithms aren't great, there's not a lot of incentive to move to them, especially before NIST has identified the winners. After that happens, we'll probably see some initial deployment of PQ certificates, starting with client support and then a few servers experimentally adding it. I doubt we'll see really wide deployment unless there is some serious pressure, e.g., from real progress in building a quantum computer. One bright spot here is the development of automatic certificate issuance systems like ACME and of automatic CAs like Let's Encrypt. It's not out of the question that we could issue new certificates to the entire Web in a matter of weeks to months (see LE's plan for this), assuming the groundwork was already in place.

The situation is a little different for the non-interactive cases, like DNSSEC or e-mail: if the signer signs with both a classical and PQ algorithm, then even if the verifier initially doesn't support the PQ algorithm, they can later go back and verify the PQ signature if support is added. This means there's more value in doing both types of signature. Note that if you receive a message which was signed only with a classical algorithm, then it's still safe to verify it even after a quantum computer exists, as long as you're confident that you received it before the computer was built and it has been kept unchanged (e.g., on your disk). It's only messages which the attacker could have tampered with that are at risk.

One of the most attractive cases for PQ signatures is software distribution, for several reasons:

• Software security is a prerequisite for basically every other kind of crypto. If you can't trust your software, you can't trust it to verify anything else. However, once you have secure software, it can be readily securely updated, if, for instance, a quantum computer suddenly appears.

• You want the signatures on software to be valid for a long time.

• Software distributions tend to be big, so the size of the signature isn't as important by contrast. Similarly, signing and verification time aren't that important because you only need to sign the software at release time (which is a slow process anyway) and the verifier only needs to verify at download.

• The post-quantum signature algorithms that we have the most confidence in (hash signatures) have some annoying operational properties when used at high signing rates, but these aren't really much of an issue for signing software.

For these reasons, it seems likely we'll see post-quantum signing for software fairly early.

Summary #

As should be clear from the above, we're nowhere near ready for a post-quantum future: effectively all Internet communications security depends on algorithms that are susceptible to quantum computers. If a practical quantum computer that could break common asymmetric cryptography were released today, it would be extremely bad; exactly how bad would depend on how many people could get one. We in principle have the tools to rebuild our protocols using post-quantum algorithms, albeit at some pretty serious cost, but we're years away from doing so, and even on an emergency basis it would take quite some time to make a switch. On the other hand, it's also possible that we won't get practical quantum computers for years to come -- if ever -- and that we'll have good post-quantum algorithms ready for deployment or even deployed long before that.