Notes on Post-Quantum Cryptography for TLS 1.2
The future is bigger than the past
Posted by ekr on 24 May 2024
As mentioned in previous posts, the IETF has decided not to add support for post-quantum (PQ) encryption algorithms to TLS 1.2. In fact, the TLS WG is taking a rather stronger position, namely that it's going to stop enhancing TLS 1.2 more or less entirely, including support for PQ algorithms:
While the industry is waiting for NIST to finish standardization, the IETF has several efforts underway. A working group was formed in early 2013 to work on use of PQC in IETF protocols, [PQUIPWG]. Several other working groups, including TLS [TLSWG], are working on drafts to support hybrid algorithms and identifiers, for use during a transition from classic to a post-quantum world.
For TLS it is important to note that the focus of these efforts is TLS 1.3 or later. TLS 1.2 is WILL NOT be supported (see Section 5).
As I wrote previously, to some extent this is a political position:
One challenge with the story I told above is that PQ support is only available in TLS 1.3, not TLS 1.2. This means that anyone who wants to add PQ support will also have to upgrade to TLS 1.3. On the one hand, people will obviously have to upgrade anyway to add the PQ algorithms, so what's the big deal. On the other hand, upgrading more stuff is always harder than upgrading less. After all, the TLS working group could define new PQ cipher suites for TLS 1.2, and it's an emergency so why not just let use people use TLS 1.2 with PQ rather than trying to force people to move to TLS 1.3. On the gripping hand, TLS 1.3 is very nearly a drop-in replacement for TLS 1.2. There is one TLS 1.2 use case that it TLS 1.3 didn't cover (by design), namely the ability to passively decrypt connections if you have the server's private key (sometimes called "visibility"), which is used for server side monitoring in some networks. However, this technique won't work with PQ key establishment either, so it's not a regression if you convert to TLS 1.3.
In this post, I want to look at what it would actually take to add PQ support to TLS 1.2 and why we probably shouldn't do it (as well as "revise and extend" that last point). This requires going into some more detail about the cryptographic primitives we are working with here as well as the history of TLS key establishment.
Static RSA #
SSLv3 (and later TLS) originally supported two main key establishment modes:
- Static RSA
- Diffie-Hellman
For a long time by far the most common mode was static RSA, shown below:
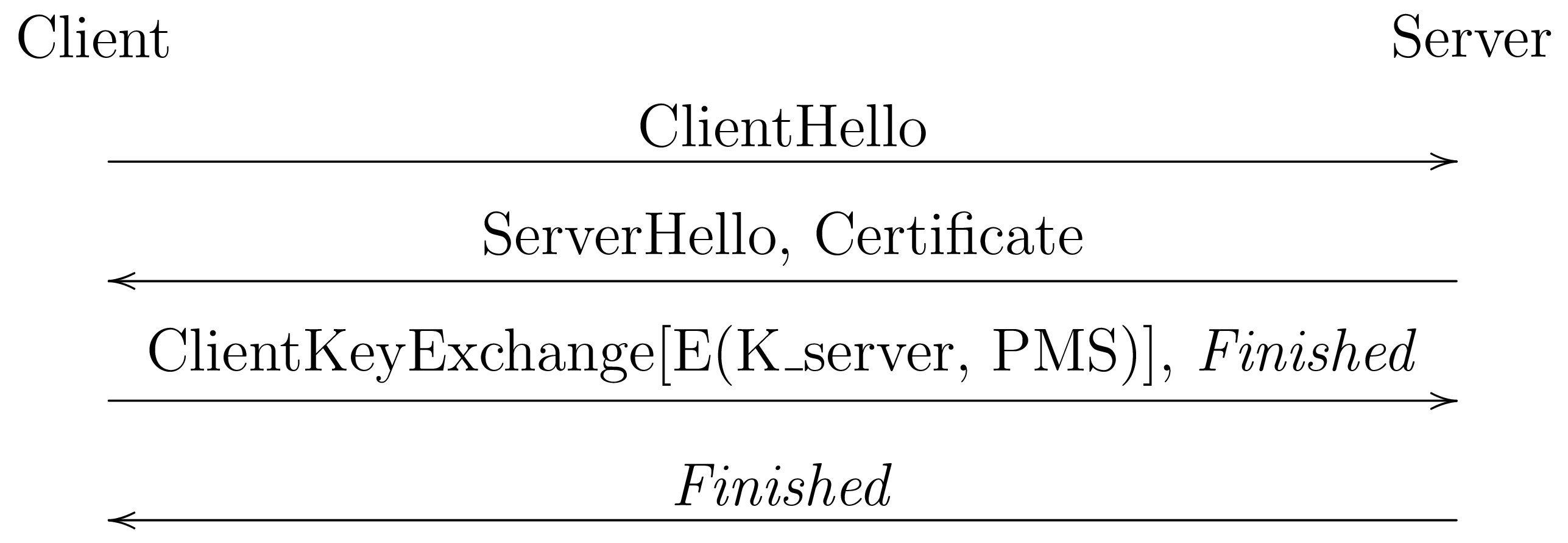
The way that this mode worked was that the server's certificate contained a public key for the RSA algorithm. The client then generated a random value (the premaster secret (PMS)) which it encrypted under the RSA public key. The server used its private key to decrypt the PMS, at which point both client and server knew it. They would each derive traffic keys from the PMS (as well as some other components of the handshake) which could be used to protect the traffic. Because the attacker doesn't have the private key it is unable to recover the PMS and therefore will not be able to communicate with the client.
This design has the property that if you know the RSA private key you can decrypt any connection protected with it. This means that an attacker who is able to obtain the private key, for instance by compromising the server, will be able to decrypt any connection that they have recorded, including connections months or years in the past (note that this is the same kind of attack we are worried about with a CRQC, except that a CRQC could recover the key from the handshake without compromising the server).
Ephemeral Diffie-Hellman #
SSLv3 also included a mode based on Diffie-Hellman key exchange:
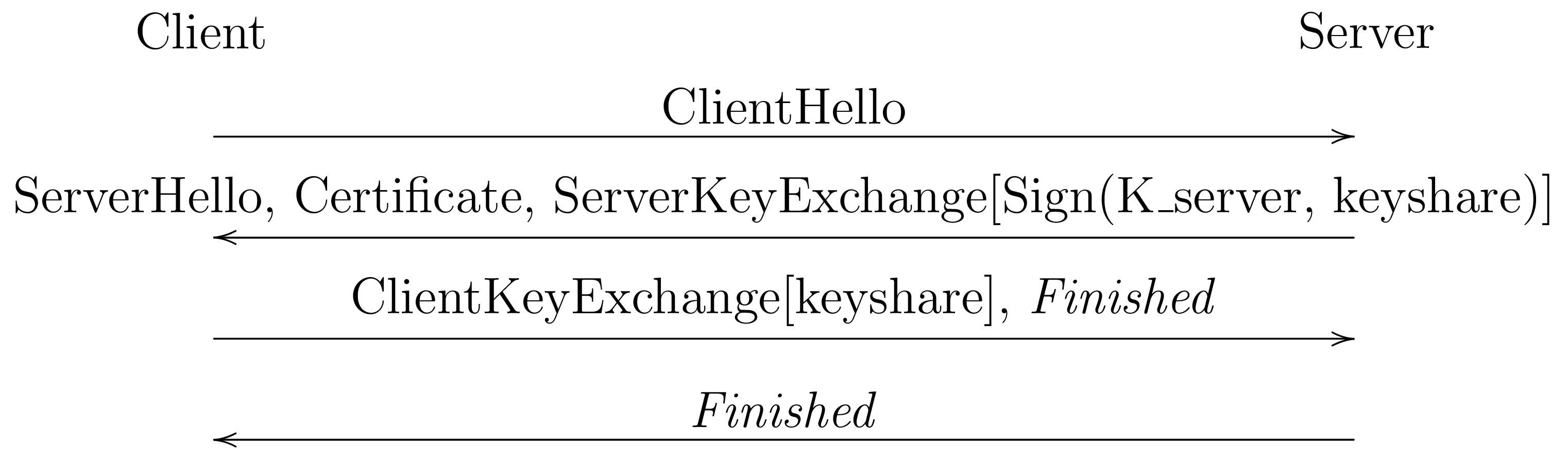
In this mode, the server generates a Diffie-Hellman key share (public/private key pair) and sends it to the client. In order to authenticate the share, it signs the share using the RSA key, thus proving that the server controls the private key. An attacker who doesn't have the private key will not be able to sign the key share and therefore cannot impersonate the server.
As long as the client and server generate a fresh key share for each connection—which isn't strictly required by the specification, but is common practice—and then delete the private part of the key share after use, then even if an attacker subsequently compromises the server's private signing key, it still won't be able to decrypt connections that happened in the past. This property is called forward secrecy (sometimes "perfect forward secrecy").
In the early days of SSL/TLS deployment, there was a lot of concern about the performance cost of the cryptography and ephemeral DH mode is much more expensive than RSA key exchange (DH itself is expensive and you also have to do the RSA signature), so most servers did static RSA in order to save CPU. Over time, however, a number of factors combined to make forward secret key establishment more attractive:
-
New Diffie-Hellman variants based on elliptic curves were developed. Elliptic Curve Diffie Hellman Ephemeral (ECDHE) algorithms were much faster than the older finite-field based algorithms and so the marginal cost of doing ECDH was much less important.
-
Servers got faster so that the cryptography wasn't as big a deal overall.
-
There was increasing concern about the practical security of non-forward secret algorithms, in part due to the Snowden revelations.
Because of the design of TLS, it was possible to incrementally deploy ECDHE. As described in a previous post, TLS negotiates the key establishment algorithm and many clients already supported ECDHE key establishment, so as soon as the server turned on ECHDE, it would automatically be able to use it with compatible clients. Moreover, RSA has the interesting property that you can use the same key pair for both encryption/decryption and digital signature, so the server could use its existing RSA certificate to authenticate to the client; all it had to do is enable ECDHE.[1]
Starting in 2013, TLS deployments increasingly used ECDHE for key establishment, as shown in the graph below.
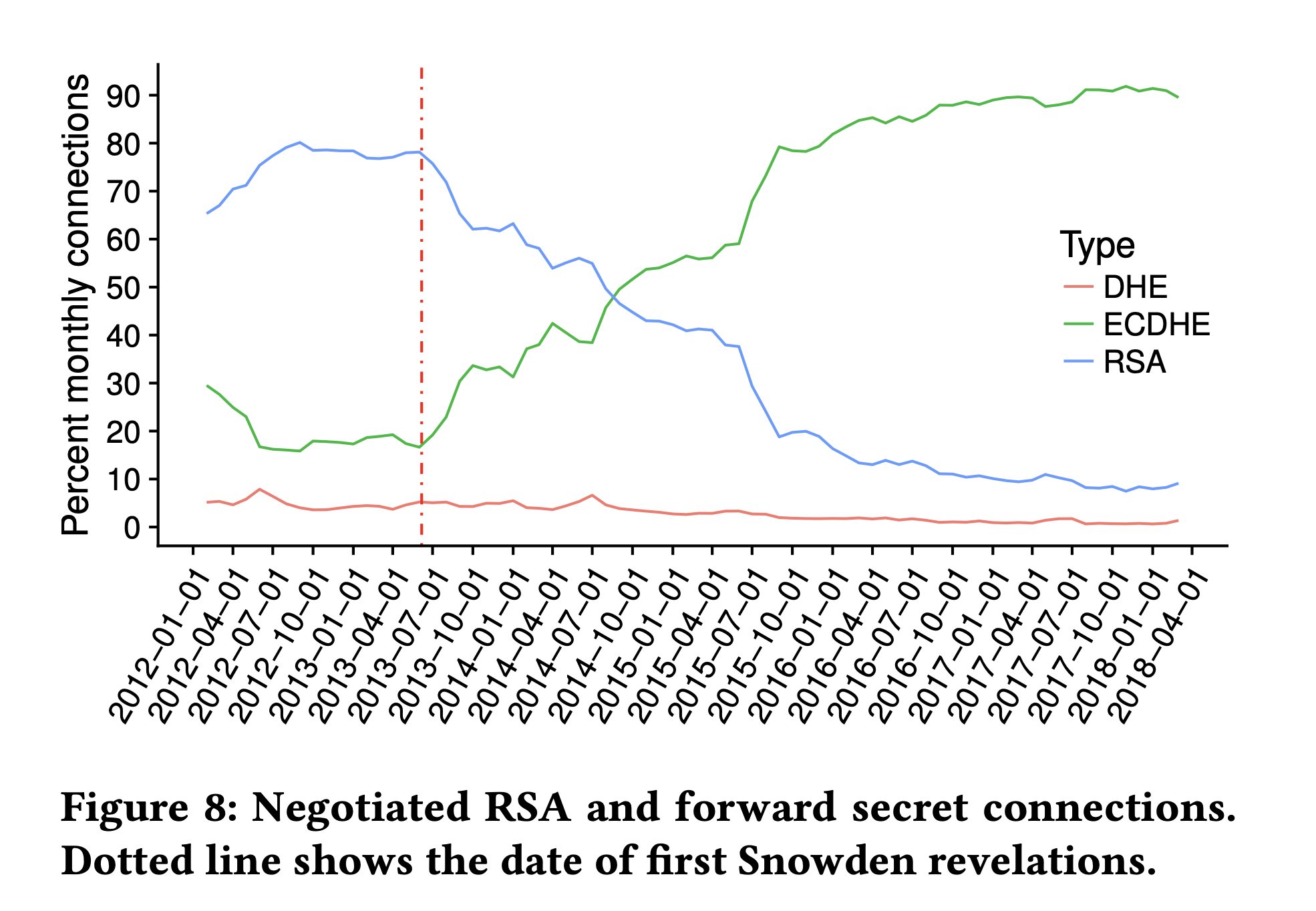
TLS 1.2 key exchange modes over time. From Kotzias et al, 2018.
Because ECDHE is so much faster, it didn't make much of a difference in terms of cost to the server to do so; in fact if you also enabled EC-based signatures using ECDSA, the total cost to the server was actually less than using RSA, though as a practical matter many servers still use RSA certificates (which should also suggest to you that the performance issues are less of a factor now then when SSLv3 was first designed).
TLS 1.3 #
When TLS 1.3 was designed starting in 2013, we had a number of objectives:
- Clean up: Remove unused or unsafe features
- Improve privacy: Encrypt more of the handshake
- Improve latency: Target: 1-RTT handshake for naıve clients; 0-RTT handshake for repeat connections
- Continuity: Maintain existing important use cases
- Security Assurance: Have analysis to support our work (added slightly later)
In order to address objectives (2) and (3) TLS 1.3 adopted a new handshake skeleton which reverses the order of the DH key shares, as shown below:

In TLS 1.3, the client supplies its key share in its first
message (the ClientHello) and the server responds with
its key share in its first message (ServerHello). As
a result, the server is able to start encrypting messages
to the client immediately upon receiving the ClientHello,
starting with its own certificate (thus concealing
the certificate from passive attackers on the wire).[2]
The client can start encrypting as soon as it gets
the server's first flight of messages, so after one round
trip, which is an improvement over TLS 1.2 in some situations.
This handshake flow is inconsistent with static RSA. Because its the client sends its key share in its first message, it needs to be able to generate it without knowing the server's public key (or key share). This works fine with Diffie-Hellman (and elliptic curve Diffie-Hellman) because the key shares are generated independently of each other, but not with RSA because in RSA the sender has to use the recipient's public key to encrypt. Moreover, because the public key is in the certificate, a static RSA-based handshake makes encrypting the certificate much more difficult, as you need the certificate in order to learn the public key and hence to establish the encryption key.
Finally, static RSA is also quite difficult to implement correctly There have also been a series of adaptive attacks on the RSA implementations in TLS stacks. The general idea is that the attacker probes the server over and over by initiating handshakes and then observing the server's behavior. It can use this technique to gradually learn secret information from the server. For instance the attacker might take the encrypted PMS from some other handshake and send variants of the message until it has recovered the PMS itself.[3] These attacks take advantage both of implementation issues with RSA and of the fact that server uses the same RSA key over and over, which gives the attacker multiple opportunities to learn small bits of inforation that add up over time (another reason why it's attractive to use a fresh key for each handshake).
Aside: Forward Secrecy and Session Resumption #
You actually need more than just forward secret key establishment to make a forward secret protocol. TLS incorporates a feature called "session resumption" in which a key established in connection 1 can be reused in connection 2, thus saving some of the cost of the key establishment (and authentication). In TLS 1.2, that key is sufficient to decrypt connection 1, so if you implement resumption you don't have forward secrecy as long as the resumption key sticks around, but in TLS 1.3 they keys are generated in such a fashion that the key to connection 2 does not let you decrypt connection 1.
But wait, there's more: some stacks implement session resumption by encrypting the resumption key with a fixed secret and sending that value to the client as a "ticket", thus removing the need for a database. Obviously, as long as that key is around, you also have a forward secrecy issue: if the attacker compromises that key then it can decrypt any tickets it has observed and learn the keys. The impact on this depends on what TLS 1.3 modes you are using. TLS 1.3 has a resumption + DHE handshake mode that provides forward secrecy for resumption while still allowing you to omit the authentication. In addition, TLS 1.3 also includes a "zero-RTT" mode in which the resumption key is used to encrypt the first packet from the client; this doesn't benefit from the resumption + DHE handshake mode because it happens before the DH key establishment.
PQ TLS #
As mentioned previously, PQ is being added to TLS 1.3 by acting as if each PQ algorithm corresponds to a new elliptic curve (group). However, in reality our PQ key establishment algorithms are much more like RSA than Diffie-Hellman. Specifically, they're Key Encapsulation Mechanisms, as shown in the figure below.
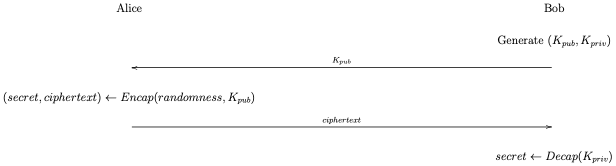
As with RSA, in a KEM Bob starts by generating a public/private key pair, (K_pub, K_priv). He sends K_pub to Alice, who then uses a function called Encap and some randomness to produce two values:
- A shared random secret value
- An associated ciphertext value
She keeps secret and sends ciphertext to Bob, who can then use the Decap function and K_priv to compute secret; at this point Alice and Bob both know it.
Just like with DH, a KEM ends up with both Alice and Bob knowing the secret, but in DH Alice can generate her key share independently of Bob as long as she knows which curve (group) he supports. I.e., it doesn't matter who speaks first and—in protocols which support it—Alice's key share and Bob's could actually cross paths. By contrast with a KEM Alice needs to know Bob's public key first, which means that Alice can't send the ciphertext until she has received the first message from Bob. This is fine with TLS 1.2, but in TLS 1.3 it's a problem because the client speaks first, so we can't use the server's public key.
In order to use a KEM with TLS 1.3, we need to reverse the direction of the KEM, as shown below. The new elements are shown in red and I've omitted the DH elements of the hybrid mode for simplicity.

- The client generates a public/private key pair and sends the
public key to the server in the
ClientHello - The server sends the ciphertext to the server in the
ServerHello
Reversing RSA #
It's actually possible to deploy RSA this way as well by having the client generate a public key and provide it to the server. Because RSA encryption is very fast and decryption is much slower, this allows you to offload work from the server to the client, which is an advantage in Web scenarios because the clients have to establish far fewer connections. EC crypto has gotten fast enough that we didn't specify this mode for TLS 1.3, but Bittau et al used this trick in tcpcrypt.
This allows you to establish a shared secret in a single round trip. As with DH, the server authenticates to the client by signing the connection transcript, which includes the ciphertext value, thus binding the ciphertext to the server's key. Like DH key establishment, TLS 1.3 key establishment also offers forward secrecy it the client generates a fresh key pair for each connection (because the server's contribution depends on the client's key pair, the server automatically generates a fresh value).
TLS 1.2 #
This brings us to the topic of PQ for TLS 1.2.
If we wanted to add PQ support for TLS 1.2, we would presumably do more or less the same thing as with TLS 1.3, namely pretend that the PQ KEM is a elliptic curve group. Just as with TLS 1.2 DHE mode, this is in the reverse direction from TLS 1.3, with server providing the first chunk of keying material (its public key) and the client generating the ciphertext and sending it to the server.
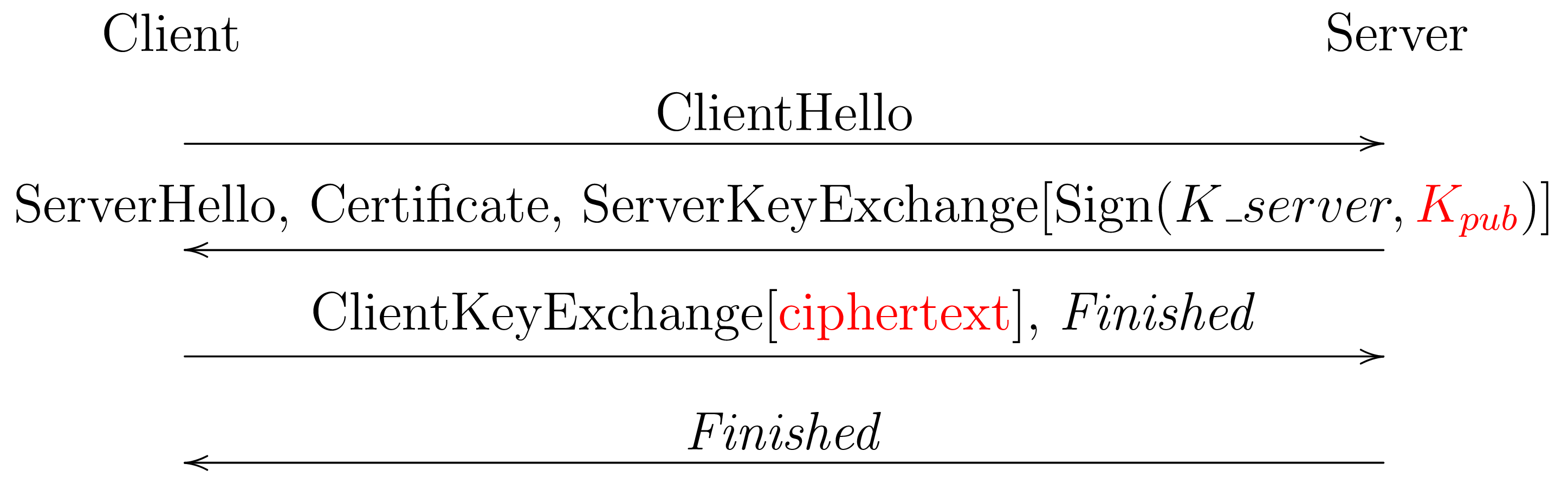
It's actually not clear that this would be safe as-is. The reason
is that TLS 1.3 binds the entire handshake transcript to the
resulting key by feeding the transcript into the key schedule
along with the initial cryptographic shared secret. By contrast,
TLS 1.2 only feeds in the random nonces in the ClientHello and
ServerHello. The result is that in some circumstances an attacker
can arrange that two connections (e.g., one from the client to
the attacker and one from the attacker to another server) have
the same cryptographic key. This property lead to the Triple Handshake Attack)
by Bhargavan, Delignat-Lavaud, Fournet, Pironti, and Strub, which was
one of the motivations for the more conservative design of TLS 1.3.
As Deirdre Connolly describes in detail,[4] KEMs have different properties than ECDHE (in some ways closer to RSA) and so we'd need to analyze precisely how to integrate them with TLS 1.2. I'm not saying it can't be done, but it's not necessarily just a simple matter of crossing out "X25519" in the specs and writing in "ML-KEM". Adapting TLS 1.3 to ML-KEM also requires some thinking but that thinking is already happening and is somewhat easier because of TLS 1.3's more conservative design. Obviously the TLS WG could do that work, but the question is whether it's worth doing, given that we are trying to transition everyone to TLS 1.3.
Why you might want to do PQ for TLS 1.2 anyway #
The basic argument for why you would want to do PQ for TLS 1.2 is that some people might find it difficult to upgrade their deployments TLS 1.3 and much easier to upgrade their TLS 1.2 deployments to do PQ. I'm generally fairly skeptical of these arguments, but I want to walk through them anyway.
Sporadically Maintained Deployments #
The broad argument is that there are a lot of environments that aren't that actively maintained and so upgrading is difficult in general and are kind of stuck on TLS 1.2. For instance, they might be using a TLS library which is updated only for security issues either because the library vendor updates it infrequently or because the library consumer is stuck on an old version.
Consider the (hypothetical) case of a TLS library which has current version 2.0 but also has a version 1.1 which is on long-term support. Version 2.0 supports TLS 1.3 but version 1.1LTS only supports TLS 1.2. A deployment which is on 1.1LTS might hope that the vendor would add PQ support to 1.1LTS even though they weren't going to upgrade it to support TLS 1.3, and that upgrading to 1.1.1LTS would be less disruptive than upgrading to version 2.0.
This doesn't apply to the Web which is generally quite up to date—and which is in the process of transitioning to TLS 1.3—but there are of course lots of environments which are much slower to upgrade and arguably might have more trouble upgrading (Peter Gutmann is one of the main advocates of this view.) I do have some sympathy for this perspective, but at the end of the day one of the costs of using software is you have to upgrade it—if only to fix the inevitable vulnerabilities—and I don't think it's unreasonable to expect people to upgrade in order to get a major change like PQ support rather than expecting the rest of the world to do a lot of work to make it slightly easier for them.
I want to emphasize that this is (almost) exclusively a software issue; as I said above TLS 1.3 is intended as a drop-in replacement for TLS 1.2, meaning that in most cases you should just be able to update your TLS stack, and get TLS 1.3 as soon as the other side updates.
Passive Decryption #
As I said, TLS 1.3 is intended to be a drop in replacement for TLS 1.2. There is, however, one notable and high profile exception, what's called TLS visibility. The problem statement goes something like this. Imagine you operate an encrypted Web server of some kind and you want to monitor traffic between users and your server. There are a number of reasons you might want to do this, such as:
- Debugging problems with your server.
- Looking for malicious activity (attacks by clients connecting to the server).
- Measuring the performance of the server on live traffic.
It's possible to do all of these things by instrumenting the server, but not all servers have great instrumentation and what if the server is the source of the problem? Another approach is to capture the traffic as it goes over the network (e.g., via port mirroring) and then decrypt it using the RSA private key. This can be done entirely passively (i.e., without interfering with the connection) and you can decrypt either in real time or by recording the traffic and then decrypting only the connections of interest. This has the advantage that you don't need to touch the server beyond getting a copy of the private key and you get to dig as deep as you want into whats going on without trusting the server.
However, these techniques don't work if you are using ephemeral Diffie-Hellman (whether of the ordinary or EC variety): knowing the server's private key allows you to impersonate the server but not to decrypt the traffic. Decrypting the traffic requires the DH private key share, which is usually generated internally by the server rather than stored on the disk the way that the long term private key is. Moreover, if the server uses a fresh DH share for every handshake—which is required for forward secrecy—then allowing decryption would require somehow sending the decryption device a copy of every key, which is obviously a lot more difficult than just a copy of a single key.
Although DH establishment became more common, even with TLS 1.2 (see above), that didn't interfere with the use of passive decryption because servers weren't required to enable it. The TLS key establishment mode as long as there is a significant population of servers which only do static RSA, clients had to support static RSA, which meant that servers could insist on it, thus making allowing this kind of passive decryption to work fine with TLS 1.2. Of course, those servers wouldn't be following best security practice in terms of protecting user traffic, but it was still technically possible.
By contrast, because TLS 1.3 doesn't support static RSA at all, it's incompatible with naive passive inspection. Of course servers could just refuse to negotiate TLS 1.3, but staying on TLS 1.2 forever isn't really an answer, especially now that the IETF has decided not to add new features to TLS 1.2. When TLS 1.3 was being finalized, a number of organizations—especially high sensitivity sites like banks or health insurance companies—raised concerns about losing this tool, but at the end of the day the TLS working group felt that forward secrecy was an important security feature and that re-adding static RSA would have been way too disruptive to the resulting protocol.
It is possible to adapt TLS 1.3 to enable passive decryption even with Diffie-Hellamn. There are at least three obvious approaches here:
-
Have the server re-use the same Diffie-Hellman key share for multiple connections. The server can then save a copy of the key somewhere (e.g., on disk) and the administrator can send a copy to the monitoring device.
-
Have the server send copies of the per-connection keys (hopefully in some secure fraction) to the monitoring device, which can use them to decrypt the connections.
-
Have the server deterministically generate the per-connection DH key shares based on a static secret and information in the connection. You then provision the monitoring device with the static secret and it can compute the DH key shares for itself.
None of these are particularly difficult to implement but they also require modifying the TLS stack in a way that isn't required to provide service to the client but only to provide the ability to passively decrypt. Moreover, options (2) and (3) also require specifying exactly how the keys will be transmitted (2) or computed (3), both of which have the potential to create severe vulnerabilities (up to perhaps complete compromise of every connection) if they are done incorrectly.
It's really important to understand at this point that what makes passive inspection work in the first place is basically just due to an idiosyncracy of the way that static RSA mode works. Specifically, you need to configure the server with the private key and the private key is also what you need to decrypt the traffic passively. This means that the administrator usually already has the credential in hand and can easily transfer it to the monitoring device without any special affordance by the server or TLS stack implementor. What we've seen over the past 8 or so years is that the implementors are much less enthusiastic about building special features to enable passive decryption. So, for instance, BoringSSL and OpenSSL don't seem to implement any of them. However, NIST has been running an initiative around this, specifying techniques (1) and (2), and it seems like some big vendors (e.g., F5), are participating. I don't know if they are actually planning to ship anything.
PQ and Passive Decryption #
This brings us to the topic of passive decryption for PQ. The obvious way to use PQ—just swapping it for DH—is not really compatible with this kind of passive decryption.[5]
This is most obvious with TLS 1.3: because the server generates its
ciphertext based on the client's public key, there's simply no server
private key to provide to the decryption device, because a fresh key
is generated for each connection. Unlike with DH, it's not even
possible to generate a single static key pair and reuse it (technique
(1) above) because the Encap() operation depends on the client's
public key.
The situation is slightly more complicated with TLS 1.2 because the server rather than the client generates the private key. In principle, the server could just generate a single ML-KEM key and use it indefinitely (similar to approach (1) above), but, as with approach (1), there is no real reason for the server to do this other than to enable visibility. Specifically:
- Re-using the same ML-KEM key breaks forward secrecy, so it's less secure.[6]
- It's actually more programming work to remember the ML-KEM key between transactions rather than just generate a new one, especially in a multi-threaded system.
- You need to build some mechanism to allow either export or import of the ML-KEM key, which you wouldn't otherwise need.
Moreover, because the most common way to deploy PQ algorithms is as a hybrid, you'd need to also do something for DH, which TLS 1.2 deployments that are set to allow passive decryption don't usually currently do now, because they just do static RSA instead. The bottom line, then, is that it's not really significantly easier to support passive decryption ("visibility") for TLS 1.2 with PQ than it is for TLS 1.3, so that's not really a very good argument for porting PQ into TLS 1.2.
The Bigger Picture #
Designing and maintaining cryptographic protocols is a lot of work, and TLS 1.3 and TLS 1.2 are different enough that it's obviously desirable only to maintain one of them even if TLS 1.3 were no better than TLS 1.2. As should be clear at this point, it's technically possible to add support for PQ to TLS 1.2, but it's not trivial. That in and of itself doesn't mean it's not worth doing, but it has to pass the cost/benefit test. For instance, there might be some important application where it was hard to swap TLS 1.3 in for TLS 1.2. However, as far as I can tell that's not true. While there are deployments stuck on TLS 1.2, they should be move to TLS 1.3 without significant impact on their existing functionality, although it might involve some inconvenience in terms of software. It would be better if they were to do so rather than the IETF community needing to maintain TLS 1.2 indefinitely.
This is not considered good practice in modern systems, but it's very convenient in this particular situation. ↩︎
Of course, active attackers can replay the
ClientHellowith their own key and get the server to encrypt the certificate to them, but this is more work than passively snooping. TLS Encrypted ClientHello addresses this issue. ↩︎There is also a version in which the attacker can extract a signature on a specific value. ↩︎
See Cremers, Dax, and Medinger for more on how to think about the security properties of KEMs. ↩︎
As an aside, there is actually a proposal called AuthKEM that adapts TLS 1.3 to use a handshake more like static RSA but with KEMs in the place of RSA. However, that doesn't change the situation for TLS 1.2, and everyone assumes that AuthKEM would be run in a forward secret mode where the client also provided a KEM public key. ↩︎
In addition, reusing the same key makes remote side channel attacks on the key (like those we see with RSA) easier. If you use a different key for each transaction, then the attacker only has one chance to learn about it so the side channel has to leak a lot more information. ↩︎