Privacy Preserving Measurement 3: Prio
Posted by ekr on 13 Oct 2021
This is part III of my series on Privacy Preserving Measurement. Part I was about conventional measurement techniques Part II showed how to improve those techniques by anonymizing data on input. This post covers a set of cryptographic techniques that use multiple servers working together to provide aggregate measurements (i.e., a single value summarizing a set of data points) without any server seeing individual subjects' data, anonymous or otherwise.
Probably the best known--and easiest to understand--of these is Prio designed by Henry Corrigan-Gibbs and Dan Boneh. Prio is already seeing initial deployment by both Mozilla and Apple/Google/ISRG. Prio allows for computing a variety of numeric aggregates over input data, as described below.
Prio Overview #
The basic idea behind Prio is actually quite simple. The client has some numeric value that it wants to report (say, household income). It takes that value and splits it into two shares (I'll get to how that works shortly) and sends one share to each of two servers. The sharing is designed so that only having one share doesn't give you any information about the original value. Every other client does the same and so now each server has one share from each client. The servers then aggregate the shares so that they have a single value which represents the aggregate of all the shares. They then send the aggregate to the data collector who is able to reassemble the aggregated shares to produce the aggregated value, as shown below:
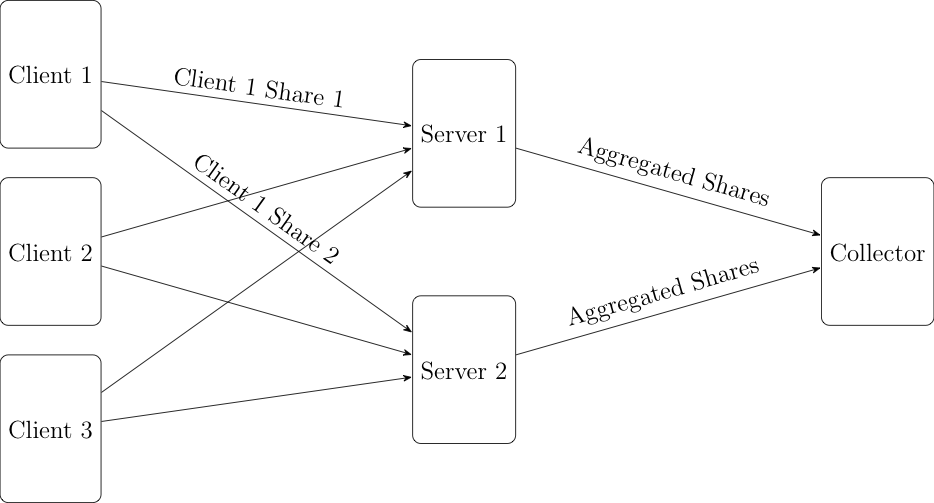
Because the shares are not individually useful as long as the servers don't collude then each user's value is individually protected. Note that I've presented this as if the servers and collector are separate, but it's just fine for the collector to run one of the servers as long as the other server is run by someone independent and trustworthy. They key privacy guarantee is that the subjects only need to trust one of the Prio servers. It's also possible to extend Prio to more servers, with privacy being guaranteed as long as one of the servers is honest, though this is somewhat more expensive.
Additive Secret Sharing #
The actual math behind splitting the secret into two shares is actually quite simple.
If we denote client i's value as X_i, then i computes:
- Generate a random number R_i. This becomes share 1.
- Compute share 2 as: X_i - R_i
The result is that server one gets all the R values and server 2 gets all of the true values - R. The aggregation function is just addition, so server 1's aggregated share is
R_1 + R_2 + R_3 + ... R_n
and server 2's aggregated shares is
X_1 - R_1 + X_2 - R_2 + X_3 - R_3 + ... X_n - R_n. If we add these together, we get (rearranging the terms because addition is commutative:
X_1 + R_1 - R_1 + X_2 + R_2 - R_2 + X_3 + R_3 - R_3 ... X_n + R_n - R_n.
Cancelling out the matching terms, we get:
X_1 + R_1 - R_1 + X_2 + R_2 - R_2 + X_3 + R_3 - R_3 ... X_n + R_n - R_n.
in other words, the sum of the original values. Magic, right?
I'm playing a bit loose with the math here: for technical reason the values have to be non-negative integers and you have to do the math modulo a prime number, p (say 64 bits or so), but none of this affects the reasoning above.
Bogus Data #
This may all seem kind of obvious, and this kind of secret-sharing based aggregation predates Prio. But I've omitted something really important: what happens if the client submits bogus data? In a conventional system where the data collector sees the raw data, they can just apply filters for data that appears to be bogus, such as by discarding or clipping outliers. For instance, if someone reports that their yearly household income is a trillion dollars, you would probably want to double check that. However, this isn't as simple a matter with a system like Prio because neither server sees individual values and the collector just sees the sum, at which point that's too late: if they total household income of 1000 households is $1,000,030,000,000 then something is clearly wrong, but you don't know whose submission to discard.[1] The complicated part of Prio is addressing this problem.
There are actually two kinds of bogus inputs:
- Values which are false but plausible (e.g., that you make $10,000 a year more than you do).
- Values which are simply ridiculous (e.g., that you make $1,000,000,000,000 a year).
It's generally quite difficult to detect and filter out the first kind of input because, as I say, it's plausible. What we want to do is filter out the second kind of bogus input.
The way Prio does this is by having the clients submit a zero-knowledge proof (ZKP). The details of how ZKPs work are out of scope for this post, but the TL;DR is that it's a proof that has two properties:
- It proves that when you add the two shares together, the result has certain properties. For instance, a submission might prove that the reported household income is between 0 and 1,000,000.[2].
- It doesn't tell the verifiers anything else about the result (hence "zero-knowledge")
Because the proof has to apply to both shares and each side only has their own share, the servers have to work together to verify the proof (actually each side gets a share of the proof).
This general idea isn't new to Prio, but what's new is that the proofs are exceedingly efficient, which makes the idea far more practical than previous systems.
Computable Functions #
The basic unit of operation of Prio is addition, which seems kind of limited, but actually is surprisingly powerful. The trick is that you have to encode the data in such a way that adding up the values computes the function you want. Here are some examples (mostly taken from the Prio paper):
-
Arithmetic mean is computed just by taking the sum and dividing by the total number of submissions.
-
Product can be computed by submitting the logarithm of the values. The sum of those submitted logarithms is then the logarithm of the product of the values (this is how slide rules work).
-
Geometric mean can be computed from product.
-
Variance and standard deviation can be computed by submitting X and X^2 and computing the average of each.
There are also algorithms for boolean OR, boolean AND, MIN, MAX, and set intersection. Somewhat surprisingly it is also possible to do ordinary least squares (OLS) regression as well.
While very powerful, this highlights an important difference between techniques like Prio and the conventional "just collect it all" approach (and to some extent the proxy approach): you need to know a lot in advance about what measurement you are trying to take because you need to have the data encoded in a way that is suitable for that measurement (or potentially even invent a new encoding). This is a general pattern in privacy preserving measurement: it's not just one technique but a set of techniques designed for taking different kinds of measurements.
Crosstabs, querying, etc. #
I've presented the above as if the servers just aggregate any given batch of client data and send it to the collector, but Prio and similar systems can also be used in an interactive setting to look at subsets of the data sets. Recall in the previous post where we had to break up household income from the other values in order to avoid de-anonymization attacks. With Prio we can do better by having each subject submit their demographic data in the clear but the household income with Prio. This produces a submission that looks like this:
[census tract, age, gender, nationality of each household member, Encrypted(income)]
The result is that each server ends up with a list of shares tagged by demographic information. This allows them to compute aggregates for subsets of the data set. For instance, you could show the data broken up by household size, or the nationalities of the members, or by both (using crosstabs. This is also enough information to do hypothesis tests like Chi-squared. The obvious cost, of course, is that the demographic information isn't private. In some cases you could have replicated this result with everything being private (e.g., if you wanted to just do OLS[3]) but in general it's more flexible if some of the data is unencrypted.
This brings us to the topic of operational mode: above I've presented things with what might be called a "push" model: the servers compute the results and send them to the data collector. However, for exploratory data analysis it's more convenient for the data collector to drive this. For instance, you might ask for a breakdown by household size and then later ask for a breakdown by household size and age to distinguish multigenerational households from families with a lot of children. There are a number of potential ways this can happen.
-
The servers can expose some sort of API that lets the data collector ask queries and get answers.
-
The data collector can collect the shares from the subjects (obviously they would be encrypted for the servers) and then just ask the servers to aggregate a given subset of the reports. This seems like an attractive model if the data collector is also one of the servers.
Each of these has some potential operational advantages; we're just starting to see the development of publicly available Prio services now (see this annnouncement by ISRG, the people behind Lets Encrypt), so it will probably take some time to get enough experience around the best practices here.
Input Manipulation Attacks #
The privacy protection provided by Prio depends on the number of individual data values being aggregated. Obviously, if you're just aggregating one value it's the same as having value itself, but if you are aggregating only a small number of values, then the level of privacy is reduced. So, clearly for Prio to work the servers have to insist on minimum batch sizes for the aggregation. Even so, however, there can be attacks based on controlling the input data.
Sybil Attacks #
The simplest version is what's known as a Sybil attack. This is easiest to mount in the model where the data collector holds the shares and just asks the servers to aggregate them for it. In this case, it takes the one submission of interest and batches it up with batch_size - 1 fake submissions where it knows the value. It can then compute the submission's real value just by subtracting its own fake values. This is a somewhat limited attack in that you need to do an unreasonable number of aggregations in order to learn a lot of people's data, but it's still concerning, especially if you only want to learn about a few people.
Repeated Queries #
Even in cases where the server just provides API access--or have some other anti-Sybil defense--it's still possible to isolate individual submissions. The basic idea is that you divide the data set into partially overlapping subsets and can then learn information about the difference in the subsets. As a contrived example, suppose we have the following data set and a minimum batch size of 2.
| Name | Gender | Height (cm) | Salary ($) |
| John Smith | M | 160cm | [Encrypted] |
| Bob Smith | M | 162 | [Encrypted] |
| Jane Doe | F | 155 | [Encrypted] |
| ... |
If I aggregate all the salary values and then ask for all the salary values for males, then I can subtract to find Jane Doe's salary. Similarly, if I ask for all the salary values of people 160cm and below I can learn John Smith's salary by subtracting it from the total. Obviously, this kind of attack is harder to mount at scale when batch sizes are large, but without any defenses there is still some privacy risk, and work on addressing this is still in early stages.
Standards Work #
All of this technology is quite new, but there's already a lot of interest. As I said above, there have already been several deployments of Prio and there is currently work on bringing Prio and some other systems to the IETF for standardization, so I expect we'll be seeing a lot more activity soon.
Next Up #
Prio and similar technologies mostly operate at the level of sets of numeric values. As we've seen above, this can be surprisingly useful, but doesn't work well when you want to collect non-numeric values. In the next post I'll be covering some technologies that allow for collecting arbitrary strings.
There's actually a more serious problem: supposing that I report a household income of -$100,000, or, because this is modular arithmetic, p-100,000, this will produce a bogus output in a way that isn't as easy to detect. ↩︎
Note that if your household income was truly >$1,000,000/year then you'd just report this as $1,000,000 ↩︎
Though even then, you really do want to look at the distribution of the data to see if the OLS makes sense. ↩︎