Verifiably selecting taxpayers for random audit

Posted by ekr on 11 Jul 2022

Note: this post contains a bunch of LaTeX math notation rendered in MathJax, but it doesn't show up right in the newsletter version. Check out the Web version where they render correctly.

The New York Times reports that both James Comey and Andrew McCabe were selected for a rare kind of IRS audit (odds of being selected about 1/20000-1/30000). These audits are supposed to be random and the Times article focuses on the suggestion that there was political influence on the selection:

Was it sheer coincidence that two close associates would randomly come under the scrutiny of the same audit program within two years of each other? Did something in their returns increase the chances of their being selected? Could the audits have been connected to criminal investigations pursued by the Trump Justice Department against both men, neither of whom was ever charged?

Or did someone in the federal government or at the I.R.S. — an agency that at times, like under the Nixon administration, was used for political purposes but says it has imposed a range of internal controls intended to thwart anyone from improperly using its powers — corrupt the process?

“Lightning strikes, and that’s unusual, and that’s what it’s like being picked for one of these audits,” said John A. Koskinen, the I.R.S. commissioner from 2013 to 2017. “The question is: Does lightning then strike again in the same area? Does it happen? Some people may see that in their lives, but most will not — so you don’t need to be an anti-Trumper to look at this and think it’s suspicious.”

How taxpayers get selected for the program of intensive audits — known as the National Research Program — is closely held. The I.R.S. is prohibited by law from discussing specific cases, further walling off from scrutiny the type of audit Mr. Comey and Mr. McCabe faced.

I don't have any particular insight on this particular case. Obviously, the chance of these particular people both being selected are very small, but there are a lot of people that former President Trump didn't like and so the chances that some of them will be selected for audits are reasonably high, so it's a bit difficult to develop the right probabilistic intuition for this, though TheUpshot gives it a valiant try.

From my perspective, however, the underlying problem is that because the process is opaque, we don't have confidence that the selection is random. What we'd really like to have is a system that is provably random. Sounds like a job for cryptography! This post is an attempt to think through the problem, both as an interesting exercise in itself and as an example of how to think through the requirements for this kind of system and then build it up in pieces.

Important disclaimer: I just wrote this up and it hasn't been analyzed by anyone else—or really by me—so it quite possibly has grievous flaws that I have not identified.

Verifiable Random Selection #

Let's start with a simpler version of this problem: we have a public list of names $\mathbb{N}$ of size $n$ consisting of names $N_1, N_2, N_3... N_n$. We want to select a random subset $\mathbb{A}$ (i.e., $\mathbb{A} \subset \mathbb{N}$) for auditing. What we need to be able to do is prove that that subset was randomly selected.

Here's the basic approach. First, you publish the following information:

1. The list in a specified order so that each name is associated with an index from $0$ to $n-1$.

2. A random number generation algorithm $R(s)$ that takes seed $s$ and generates values in the range $[0..n)$ with equal probability.

3. A method for computing the seed that is (a) verifiable (b) unpredictable at the present time and (c) not under the control of any plausible set of people who might cheat.

The first two of these are straightforward, but the last is more complicated. We need some mechanism that's easy to explain but also verifiably fair. One simple solution, used by the IETF for selecting volunteers for it's nominating committee is to use preexisting random numbers like lottery results or the low order digits of stock prices. I cover some other approaches later.

Once you have the random seed $s$, things are pretty straightforward: you run $R$ iteratively to generate numbers in the appropriate range. Each number corresponds to a selected list entry. Typically, you sample without replacement, so if you select an entry that's already been selected, you just generate a new number and try again.^[1] The code looks something like:

R.seed(s);
selected = [];

while (remaining > 0) {
  do {
      candidate = R.next();
  } while (candidate in selected);
  
  selected.append(candidate);
  remaining -= 1;
}

It's worth taking a moment to see why this works. Steps 1-3 are all fair, which is to say that if you assume a random $s$, then any set of selected values are equally likely. This means that unless you know $s$ in advance, it's not possible to predict who will be selected. It's also not possible to modify the order of the list or the detailed structure of the random number generator^[2] in order to select one set of people over another. It's critically important that steps 1-3 be run before $s$ is known, otherwise you could tamper with the list order or $R$ in order to get the effect you want. The jargon here is that you commit to them in advance, and that they can't be changed afterwards. This also gives the public the opportunity to verify that the list of names is correct and that random number generator $R$ meets the correct requirements. For the same reason that they need to be committed to in advance, if you allow changes—even to correct errors—after $s$ is known it's too late because someone who detected an error might choose to strategically disclose it or not once they saw the outcome of the selection.

This simple design has several of deficiencies which make it less than ideal for sampling taxpayers. First, it just bootstraps off an existing source of randomness, but why do you think you can trust that? That's relatively easy to repair, as discussed below. More importantly, it involves publishing the identities of every taxpayer who might potentially be audited. This is already not ideal, but gets even worse if you want to oversample some set of taxpayers (e.g., those who have higher net incomes), or exclude some people (e.g., those who didn't pay income tax). For obvious reasons, this shouldn't be public information. Moreover, because a lot of people have the same name, you need to identify them somehow, and that probably means their social security number (SSN). SSNs are a terrible identifier, but they're also very widely used as a form of authentication—how often have you been asked for the last 4 digits of your social as an authenticator?—so having them be public is bad news.

One possibility would be to have the list consist just of SSNs. This would ordinarily be a bad idea because, as noted above, SSN are sensitive, but in practice a very large fraction of 9 digit numbers are actually valid^[3]: there are $10^9$ (1 billion) possible 9 digit numbers and about 330 million people in the US, so any given random 9 digit number has about a 1/3 chance of being a valid SSN for someone currently alive, so having a list of valid numbers isn't that informative; it's the binding between SSNs and people's names that is sensitive. However, it's still a problem if you want to do weighting by income because you don't want someone who knows your SSN to be able to infer your income bracket.

Moreover, any cleartext list has the problem that the public can determine who was audited, which seems suboptimal. We'd like a solution that allowed you to verify that selection was fair but not who was audited. More precisely, anyone should be able to verify that the selection was fair and people who are selected should be able to verify that they—but nobody else—were selected.

Hashing Taxpayer Identities #

The obvious solution is just to hash the identities. So, we start with a list of taxpayer identities (e.g., SSNs or the pair of name and SSN) and hash each entry to make a new list, as shown below:

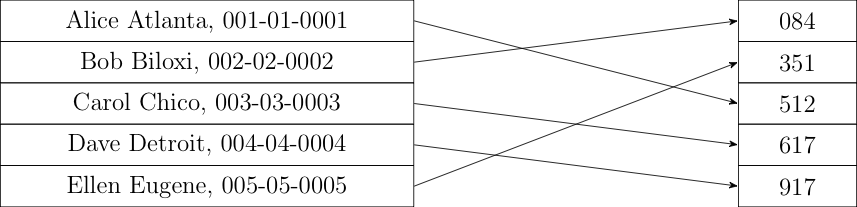
You then just select out of the original list using the method I described above. The IRS has the original list and can therefore easily determine who is to be audited. Anybody can verify that that computation was done correctly, and the people who are selected can verify their selection by hashing their identity and seeing that it matches one of the selected hashes.

Note that I've also reordered the hashes by sorting them in numeric order. This destroys any initial structure in the list. If we don't do this, then people could look at which hashed list entries had been selected and potentially learn information about who had been selected for the audit. For instance, if there are 150 million taxpayers and the first one audited has index 500,000, it's unlikely it's Aaron A. Aaronson. Because the hashes are effectively random with respect to their inputs, just sorting the hashes numerically produces a list whose order is unrelated to the original order.

This is a simple and obvious solution, but unfortunately it's also wrong. The problem here is that the input identity values are low entropy and the hash is public. Because there are only $10^9$ SSNs, it's easy to compute the hashes for any name and all possible SSNs and just compare them against a given hash. This costs roughly $2^{30}$ computations per name, which is quite cheap. There are at most $2^{29}$ distinct names in the US (there are fewer than that many people and of course many people have duplicate names), so computing every possible name/SSN pair costs less than $2^{60}$ computations, which is a lot but not at all out of the realm of a dedicated attacker.^[4] Moreover this computation just needs to be done once and then you have the whole table.^[5]

Commitments #

I said above that part of the problem here was that the hash was public, so what if we make it private instead. One way to do this is with what's called a commitment. A commitment is like a hash, except that it depends on an unknown secret value, so that it's not possible to compute the commitment without knowing it. I.e.,

$$ Commitment = C(secret, Message) $$

The way you use a commitment is that you publish the output of the commitment but not the secret value. Then you can prove that the commitment matches a give message by revealing the secret value, at which anyone can compute the commitment for themselves. Constructing a secure commitment scheme is somewhat complicated, but you can think of it as hashing the concatenation of the secret and the message, e.g.,

$$ C(secret, Message) = H(secret + Message) $$

A commitment-based scheme works more or less the same as a hash-based scheme, except that the IRS generates a new secret for each user and stores it with the input table. It then can generate the table of commitments, as shown below:

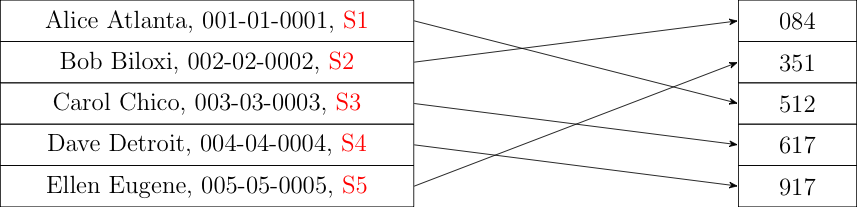
Selection of the taxpayers to be audited proceeds exactly as with hashes. The result is that anyone can verify that the list of hashed (committed) identifiers to be audited was generated correctly. In order to convince a given taxpayer that they were selected you show them their associated secret. They can then compute the commitment themselves and verify that it's on the selected list.

This solves the problem of keeping the selected list secret, but at the cost of verifiability. Yes, you can verify that the right commitments were selected and a given taxpayer can verify that they correspond to a specific commitment, but you can't verify that the original commitments match the right list of taxpayers. For instance, suppose that the IRS wants to make sure it always audits Alice Atlanta. All it has to do is make a list that mostly consists of commitments for Alice Atlanta, like so:

Obviously, this greatly increases the chance that Alice will be selected. Because all the commitments use different secrets, they are all distinct even though they are for the same identifier, and so it's not possible for anyone other than the IRS to see that there are duplicate inputs. When Alice is selected, the IRS can just reveal the relevant commitment and she doesn't know that there were other commitments for her.

One interesting thing that can happen is that Alice might be selected twice (this can just happen randomly). This isn't something that ordinary people can detect: non-selected people just see the total number of selectees and the IRS can just pick one of the commitments it selected for Alice and show her and discard the other one. Obviously, you could have an internal check that verified that the right number of people were audited, but that's not publicly verifiable.

Verifiable Random Functions #

The source of the non-verifiability in the commitment approach is that because each commitment uses a fresh secret, there there isn't a unique mapping from identities to commitments. Fortunately, there is a function which has the properties we need, namely:

1. There is a unique mapping from identities to commitments
2. The mapping can't be computed by third parties
3. The mapping can be verified by third parties

What we need is what's called a verifiable random function (VRF). A VRF works by having a secret key $K_s$, a public key $K_p$, and a pair of functions $VRF()$ and $Verify()$. The function $VRF$ outputs two values, the output value and a proof of correctness of the output value, like so^[6]

$$ (Output, Proof) = VRF(K_s, Message) $$

The $Proof$ can be used as an input to the function $Verify(K_p, Output, Proof, Message)$, which returns $True$ if and only if $Output$ and $Proof$ match the $Message$. The result is that you can only compute the VRF if you know $K$ but anyone can verify the VRF given the triplet $(Output, Proof, Message)$. The details of how to construct a VRF are out of scope for this post, but see Goldberg, Reyzin, Papadopoulus, and Vcelak for a specification describing several VRFs.^[7]

In this case, we would use the $Output$ as the value in the "hashed" list used for the selection and keep the $Proof$ secret. Because the VRF is deterministic, any input value can only correspond to one output, thus preventing the kind of duplication attack we saw with commitments. As before, anybody can verify that the selection algorithm was run correctly, and you prove to the selectee that they were on the list by giving them the corresponding proof, which they can verify for themselves.^[8]

Oversampling #

Having multiple entries for a given taxpayer can be used as an attack but is also potentially useful, for instance if you want to have higher-income taxpayers be more likely to be audited. One possibility here is just to have multiple lists with different selection probabilities, but this gets clumsy if you have a lot of different selection levels and also reveals the distribution of the number of taxpayers in each cohort.

An alternative design is to have multiple entries. For instance, suppose that we have two groups, Rich and Poor and we want Rich people to be selected twice as often as Poor people. This can easily be achieved by simply having two entries for each Rich person. We can't do this directly with a VRF, but we can just have the input to the VRF be the taxpayer's identity plus a counter. E.g., for Alice we could have Alice Atlanta: 1 and Alice Atlanta: 2. This doubles the chance of selection, and when either of these identities is selected you just have to prove to Alice that she was selected and that the counter in question is within the appropriate range (in this case, either 1 or 2). Nothing stops the IRS from creating an entry for Alice Atlanta: 3 but if they show it to Alice, she can contest it because her maximum index should be 2, so it's not really different from having having Alice Schmatlanta; it's just an entry that doesn't correspond to anyone. The same strategy can be applied for any set of ratios, though things get a bit messy if you want to (say) have one set of taxpayers be audited 1% more than another set, because you need them to have 100 and 101 entries respectively.

One difficulty with this strategy is that it doesn't properly handle multiple selections. For instance, we might select both Alice Atlanta: 1 and Alice Atlanta: 2. In practice, these audits are very rare, so this is pretty unlikely and so it's probably easiest to just do one less audit, but I think you can solve this problem with another layer of hashing. Specifically, to compute the list entries you would compute

$$ H(VRF(K_s, Identity) + Counter) $$

If you get a duplicate during the sampling process, you reveal the inner VRF output and prove that they two selected entries correspond to two hashes with different counters. This doesn't reveal any information about the rest of the structure of the list. Note that the attacker can't just iterate through hash inputs because the VRF output is high entropy even if the identities are not.

Generating Random Seeds #

Above I sort of handwaved the random seed generation problem. For a number of options it's fine to depend on some sort of untrusted source. However, you don't need an external randomness source. The basic idea is that you have a set of parties who get to contribute randomness to the seed. Each party $i$ generates a random share $R_i$ and you concatenate them in some pre-determined order and use that as the random seed.

If each party generates their value independently, then as long as at least one of the values is random, the whole output will be random. The problem here is the word independently. Suppose that there are $n$ parties and parties $1..n-1$ all publish their seeds. Party $n$ can then iterate through a bunch of seeds until it finds one that produces the set of random numbers it wants. Fortunately, we have a pre-existing tool for fixing this, the commitment. Effectively we have a two-round protocol:

• Round 1: everyone publishes their commitments to their shares $R_i$
• Round 2: everyone reveals $R_i$ and show that it matches the commitment

This protocol will work as long as there is at least one party who (1) generates a random value and (2) doesn't collude with the others by revealing their value before the commitments are published.

There are, of course, a few logistical problems here: who are the parties? What happens if they publish their commitments but then decide not to reveal $R_i$ (for instance because they don't like the resulting output)? These are real problems for some instantiations of this kind of scheme, but in practice it's probably fine to just have a small number of trusted parties (e.g., the US Government, some of the Big 5 Accounting Firms, etc.) who would suffer severe reputational damage if they were to cheat or refuse to reveal their share.

Another approach that people sometimes use for public verifiability is to have people roll dice. Cordero, Wagner, and Dill describe procedures for this in a classic paper called The Role of Dice in Election Audits.

Note that you can use all of these systems together: you just run them all, glue the data togetether (e.g., by concatenating it in a predetermined order), and feed it into the random number generator as the seed.

Drawbacks #

This is not a perfect system. First, like many cryptographic systems, it's fairly complicated and the math required to convince yourself that it behaves as advertised is way beyond most people. On the other hand, people regularly trust their credit cards, passwords, instant messages, and importantly tax returns to systems no more complicated than this and that are based on pretty similar cryptographic primitives. Moreover, the current system is totally unverifiable, so almost anything is an improvement.

From the technical side, I'm aware of at least one notable deficiency: while this system prevents the IRS from inappropriately auditing someone, it doesn't prevent them from making sure someone doesn't get audited; all they have to do is omit them from the list. In our original design, this was easily detectable, but once we mask taxpayer identities with the VRF, it's no longer possible. I'm not aware of any simple way to fix this, because you would need a list of the valid identities to compare to, which is something I'm trying to avoid. With that said, I'm not sure how serious this is: if the IRS wants to cheat it can just not audit someone that gets selected. You need some (non-transparent) internal procedures to detect this case, so maybe you can use them to ensure the list is complete as well.

Final Thoughts #

Taking a step back from this particular case, there are a lot of types of data processing that have real impact on our lives but where we just have to trust that the entities—whether governments or corporations—are handling it correctly. This includes a broad range applications from voting to medical records to income taxes to your search history. In each of these cases, mishandling of the data could lead to real harm; even if you trust the current entity to behave correctly there is no guarantee that they will do so in the future or that their systems will not be compromised.

The good news is that we are starting to have the technologies to allow the public to verify that these processes are conducted correctly. A good example from another field is risk-limiting audits for election verification, as pioneered by Philip Stark—which also requires some method of verifiably sampling, albeit a simpler one— which is actually starting to be used in real elections. In general, this is a good development: it's important to have good policies and trustworthy institutions, but even better if we don't have to trust them, especially in cases like this where correct behavior is important for democratic governance.