Privately Measuring Vaccine Doses

Posted by ekr on 25 Jan 2022

Note: this post contains a bunch of LaTeX math notation rendered in MathJax, but it doesn't show up right in the newsletter version.*

Anyone can go to the CDC Web site and find out the status of the US COVID vaccination effort. Unfortunately, due to privacy controls in the CDC's data collection(see footnotes), this data seems to be less accurate than we would like:

To protect the privacy of vaccine recipients, CDC receives data without any personally identifiable information (de-identified data) about vaccine doses. Each record of a dose has a unique person identifier. Each jurisdiction or provider uses a unique person identifier to link records within their own systems. However, CDC cannot use the unique person identifier to identify individual people by name. If a person received doses in more than one jurisdiction or at different providers within the same jurisdiction, they could receive different unique person identifiers for different doses. CDC may not be able to link multiple unique person identifiers for different jurisdictions or providers to a single person.

These inaccuracies are made somewhat less apparent by the fact that the CDC caps ("top codes") estimates of vaccine coverage at 95% (formerly 99%), so you don't see reports where more people in an area are vaccinated than actually live in that area:

CDC has capped the percent of population coverage metrics at 95%. This cap helps address potential overestimates of vaccination coverage due to first, second, and booster doses that were not linked. Other reasons for overestimates include census denominator data not including part-time residents or potential data reporting errors.

As I understand it, the situation here is that the data reported by states is roughly accurate, as long as you don't get into people who got doses out of state, but the CDC data is less so because of these privacy measures. For instance, the CDC's data shows that 40 different states have 95% of people 65+ with at least one dose, which not only doesn't help you distinguish between California and Iowa but actually seems to be wrong for California as well. Here's a comparison of the California and Federal Data for 65+.

It's somewhat hard to square this data, and the percentages may just be about the size of the eligible population, but the raw numbers should at least agree. At least part of what's going on seems to be that doses are being misattributed (e.g., boosters marked down as first doses) and CDC not having ground truth doesn't help us debug. A number of commenters have been quite critical of these privacy measures and their impact on the accuracy of the data. For instance, here's political blogger Matt Yglesias:

Besides this, the stated reason for collecting such bad data is not to allow people to get illicit boosters, it’s to protect their privacy. As I wrote in “They deliberately put errors in the Census,” I am very skeptical that the privacy value of having the government do inaccurate record-keeping is high.

I suspect I'm more sensitive to privacy issues than Yglesias, but I'm also not sure this is the right tradeoff. In this case, especially, that the states (and of course, probably the health insurance companies) seem to have non-anonymous measurements of who got vaccinated and when, so it's not clear why it's that big a privacy increment to deny this data to the CDC. Moreover, the states can't easily get more private because they seem to be using that information to implement their vaccine passport systems. For instance in California or New York, you can just input some identifying information and download your vaccine passport; this obviously wouldn't work if this data is stored without identifiers. With that said, I can also see the argument that you don't want the federal government having this information and—unlike the states—it's using it for statistical and not operational purposes, so it's worth asking whether it's possible to improve the situation. As usual, sounds like a job for cryptography.

Anonymously Measuring Vaccination Rates #

The underlying problem here is that we want to be able to measure the rate of various kinds of vaccination in each demographic region. This seems to require that we be able to:

1. Associate vaccine doses with demographic information like where they were given, where the patient lives, age of the patient, etc. This allows you to measure geographic deployment rates.

2. Associate multiple doses given to the same person so that you don't say obviously wrong things like 200% of people in California have gotten first doses and nobody has gotten a second dose.

The first requirement is actually readily addressable with privacy preserving measurement techniques like Prio (see here for my writeup), but it doesn't do a good job of linking up multiple doses. One could imagine having a different counter for "first dose", "second dose", etc. with the states reporting each dose appropriately. However, part of the problem seems to be that the status of each dose is being inaccurately reported, both because of errors and because some people actually deliberately concealed or at least didn't disclose their vaccination status, e.g., to get an early booster.

If you didn't care about privacy, you would address this just by having each dose associated with some permanent identifier (ID) like personal name or—even better for accuracy but worse for privacy—social security number. You then would just have a list of doses, dates, and identifier and could sort things out in the obvious fashion by grouping by identifier and then counting. But of course the problem with this is that the identifier is, well, identifying, which is what we are trying to avoid. So, what you want is a stable pseudonymous identifier (PID) derived from this information (thus allowing grouping) but that can't be reversed to give the input information (thus protecting user privacy).

Some things which won't work: hashes, PRFs, and OPRFs #

The obvious thing to do here is to just hash the data, but that's clearly not going to work: the cryptographic guarantees around hash functions only apply when the input space is large, but in this case, the input space will be quite small (for instance, there are only 10⁹ SSNs, so it's trivial to compute the hashes for all of them, and the space of names is not that much larger). This means that the CDC could easily make a table of all the possible identifiers and who they belong to.

The next natural thing to try is some kind of keyed one-way function like a Pseudorandom Function (PRF), but the problem then becomes who can compute this function. PRFs depend on a key, and if the CDC knows the key then it's not better than a hash function. But as a practical matter, if every state has the key, then it's a stretch to think that the CDC will not get it or convince some state employee to run the PRF for them on the (again, small) set of potential names.

Recently, it's become common to throw oblivious PRFs (OPRFs) to this kind of problem. An oblivious PRF is like a PRF except that it can be computed on a blinded version of the input. This means that you can set up a server which will compute the OPRF for people without seeing it, like so:

In this version, the state would blind the patient's name and send it to the OPRF Server, which would compute the OPRF on the blinded input and then return it. The state then unblinds the result to get the PRF on the original input. This has two important properties:

1. It can't be computed without the key.
2. The OPRF service never sees both the input and the output because they are blinded. The state of course does get the output (the PID) and sees the input.

In the full system, then, health authorities, states, etc. would collect the patient's ID and ask the OPRF server to map it to the pseudonymous PID, and then send the information to the CDC. This is slightly better, but not much because the OPRF service is an oracle that lets a lot of people map the client true identifier to the PID, and so you need to tightly control access to that service. But a lot of entities (at least states, but also maybe local health departments) are going to have access to that service, which makes the problem hard, as any of them can be used to unmask people. Moreover, it's kind of an inconvenient interface for the states because they want to just submit their data, not have some complicated mapping process that they do pre-submission.

Interoperable Private Attribution #

The underlying problem here is that we need a way to map $ID \rightarrow PID$ that can't just be used by the CDC. Otherwise, they can just try candidate $ID$ values until they get a $PID$ match. Recently, Erik Taubeneck (Meta), Ben Savage (Meta), and Martin Thomson (Mozilla) published a new multiparty computation technology called Interoperable Private Attribution (IPA). As the name suggests, it's designed for measuring conversions in online advertisements, and I may write about that later, but the basic ideas can be adapted for measuring vaccine uptake.^[1]

The general idea behind IPA is that we have a service which is kind of like an OPRF in that it takes in an encrypted identifier and outputs a blinded identifier which can't be tied back to the original input (which is essentially the same problem we are trying to solve). However, if we just emit a blinded identifier in response to an encrypted identifier, the service can be used as an oracle to compute the mapping to blinded IDs. In order to prevent that, the service actually has to take in a group of encrypted identifiers and shuffle them somehow (e.g., by emitting them in a batch). This gives you an interface more like this:

Note that this interface could take identifies in as a batch and then shuffle the batch or one at a time but then buffer them; it just has to make it hard to determine which input goes with which output. In addition, we don't want one entity (in this case the OPRF server) to be able to unmask everyone, so we need to distribute the computation over multiple servers, like so:

Note that the precise communication between servers is a bit complicated. The first server actually only partially decrypts and then blinds and passes things to the second server. Details can be found below.

There are a number of ways to use a service like this. The most obvious is simply to have each vaccine dose be a single report, and then submit them to the service and look at the output in batches. The result will just be a set of delinked, shuffled identifiers, like so:

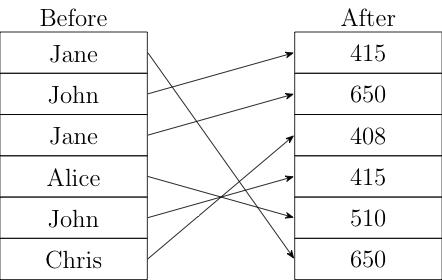
Now you can just count how many times each identifier appears; identifiers which appear once are single doses, twice are double doses, thrice are boosted etc. If you take the data in daily batches, you can also estimate the amount of time between doses by looking at what day each identifier is reported. You can also do geographic distributions by sending each jurisdiction in separately. In the original IPA proposal, the way things work is that all the encrypted reports were sent to a "Consumer" which gets meta-information like the site the report came from. The consumer could then ask the service to aggregate only a subset of the data.^[2]

There are two important properties of this system that might not be immediately obvious. First, the blinding and shuffling process doesn't preserve meta-information: it just emits the identifiers. If you want to learn about subsets of the data, you need to process the data in chunks (e.g., one state at a time.) The IPA authors have been working on how to carry some meta-information along with the reports, but it's a somewhat complicated problem, as the blinding process would destroy it, and they haven't published a design for this feature.

Second, if you allow the consumer to do a lot of queries of different subsets, then they can use that to extract information about the original data (see here for more). This requires you to restrict the number of different queries, or potentially to just commit in advance to what you will do (e.g., just down to counties on a daily basis). Sybil attacks in which the consumer injects fake queries are also possible, but can be prevented by having the jurisdiction sign their reports.^[3]

IPA Technical Details #

This section provides technical details. I've attempted to make them mostly accessible and can be understood based on high school math^[4] , but they can also be skipped if necessary. This section will not render properly in the newsletter because I use MathJax to render LaTeX. Click here to see it rendered on the site.

Note: in ordinary integer math, given $g^a$ and $g$ it's easy to compute $a$ but we're going to be doing this in an elliptic curve where that computation is hard. Everything else is pretty much the same, but just remember that part.^[5]

The service is implemented by having a pair of servers, $A$ and $B$. Each has a Diffie-Hellman key pair, which is to say a secret value $x$ and a public value computed as $g^x$. We'll call $A$'s key pair $(a, g^a)$ and $B$'s pair $(b, g^b)$. Each server also has a secret blinding key $K_a$ and $K_b$. These servers are operated by different entities who are trusted not to collude. However, if either service behaves correctly then you're OK. The service then publishes a combined public key $g^{a+b}$ which can be computed by multiplying the public keys: $g^a * g^b$ (if you remember your high school math!).

In order to submit an ID $I$, the sender first encrypts it. It generates a random secret $x$ and computes: $g^{x(a+b)} = {(g^{a+b})}^x$. Note that we're using the service combined public key and the sender's private value $x$, so the result is a secret from attackers who don't know either $x$ or $a+b$. It then multiplies $I$ by this value and sends the pair of values (this is just classic ElGamal Encryption, but to the key $g^{a+b}$):

$$g^x, I * g^{x(a+b)}$$

Importantly, this second term can be broken up into a part involving only $a$ and a part involving only $b$. I.e.,

$$I * g^{x(a+b)} = I * g^{xa} * g^{xb}$$

Again, this is just high school math. These values then get sent to $A$ (or $B$, it doesn't matter), who computes $g^{xa} = {(g^{x})}^a$ (recall it knows $a$). It then divides the second part by $g^{xa}$:

$$I *g^{xb} = \frac{I * \cancel{g^{xa}} * g^{xb}}{\cancel{g^{xa}}}$$

This cancels out the $g^{xa}$ term, leaving you with just a term that involves $b$, and thus the pair:

$$g^x, I * g^{xb}$$

$A$ then blinds this value, by exponentiating both values to $K_a$, giving:

$$(g^x)^{K_a}, (I * g^{xb})^{K_a}$$

We can flatten this out to give:

$$g^{x * K_a}, I^{K_a} * g^{(xb)(K_a)}$$

$A$ batches these values up with other inputs it has received, shuffles them, and sends them to $B$. $B$ takes the first term and computes $(g^{x*Ka})^b = g^{x * K_a * b} = g^{(xb)(K_a)}$. It then divides the second term by this value, to get:

$$I^{K_a} = \frac{I^{K_a} * \cancel{g^{(xb)(K_a)}}}{\cancel{g^{(xb)(K_a)}}}$$

Finally, $B$ blinds the value by taking it to the power $K_b$, this giving us:

$$I^{(K_a)(K_b)} = (I^{K_a})^{K_b}$$

That was a lot of math, but the bottom line is that the actual identifier $I$ (e.g., the SSN) has been converted into a new blinded value, with (hopefully) the following properties:

1. Neither $A$ or $B$ ever saw $I$
2. $A$ sees the input encrypted version but doesn't learn the blinded version.
3. $B$ sees the blinded version but doesn't learn the encrypted version.
4. You need to know $K_a$ and $K_b$ to compute the blinded version of $I$.

Disclaimer: The IPA documents were just published recently, so I don't think they have seen enough analysis to prove they are secure. Here I'm just describing how it's supposed to work.

Limitations #

Like any privacy preserving measurement system, this has some limitations, in particular in the area of flexibility. For instance, this will only properly attribute vaccine doses when there is an exact match on the original identifier. This will work OK if the identifier itself has a single form, like a social security number, but what if you use name and birthday. In that case, "John Smith" and "John H. Smith" will look like different people. If you had people's actual names, you could try to correct this kind of error by looking for close matches at approximately the right time, but IPA isn't "distance preserving" in that two similar inputs A and B are not likely to have blinded versions which are similar, so you can't make this kind of correction later.

Another problem is that in the form I've presented it, you're losing information like the kind of vaccine, so you can't easily ask "how many people started with J&J and then boosted with Moderna." There are some potential avenues for making this work, for instance to carry metadata along with the identifier, and that's probably possible, but making that work is more complicated than the protocol I described above.

Finally, because repeated queries can be used to determine which reports belong to which individuals, you need to limit the number of different kinds of queries you do. This is probably fine if you want to just record the number of doses of each type in a given region, but less fine if you want to do some kind of deeper research. Of course the states can do that analysis now because they have accurate data, but if you want to do national scale analysis or you want it done consistently, that's not that great an option.

Summary #

Given the fact that the states are collecting directly identifying data about vaccination, I suspect it's a bad tradeoff to conceal this data to the CDC: the privacy improvement seems modest and the effect on accuracy is real. However, if we are going to take it as a hard requirement that the CDC not learn identifying information, then we can use Privacy Preserving Measurement techniques to get substantially better accuracy than the CDC seems to be achieving today.