Overview of Interoperable Private Attribution
Posted by ekr on 15 Feb 2022
Note: this post contains a bunch of LaTeX math notation rendered in MathJax, but it doesn't show up right in the newsletter verison. You should mostly be able to follow along anyway except for the "Technical Details" section and the Appendix (which is part of why it's an appendix) so you may want to instead read the version on the site.
Recently, Erik Taubeneck (Meta), Ben Savage (Meta), and Martin Thomson (Mozilla) recently published a new technique for measuring the effectiveness of online ads called Interoperable Private Attribution (IPA). This has received a fair amount of attention—including some not so positive comments on Hacker News. I've written before about how to use a variant of this technology to measure vaccine doses, but I thought it would be useful to walk through how IPA works in its intended setting.
Attribution and Conversion Measurement #
For obvious reasons, advertisers and publishers want to know how effective their ads are. The basic tool for this is what's called "attribution" or "conversion measurement", Suppose I see an ad for a product on a news site and click on it, taking me to the merchant, where I subsequently make a purchase. This is called a conversion, and advertisers want to know which ads convert—and how often—and which ones do not.
At the moment, conversion measurement is mostly done with cookies, as shown in the figure below:
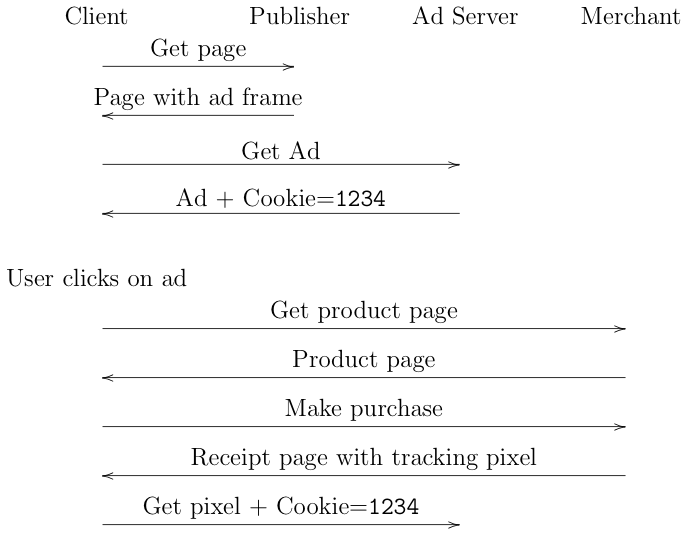
Let's walk through this in pieces. First, the client visits the
publisher site. The publisher serves the client a Web page
with an IFRAME
from the advertiser[1]
(reminder: an IFRAME is HTML element that allows one a Web page to
display inside another Web page, even from two different sites).
When the advertiser sends the page, it also sends a tracking
cookie to the client, in this case 1234.
The user views the ad (an impression) and clicks through, which takes them
to the merchant. In this case, they just make
an immediate purchase, but they might also shop around on the
site or even go away and come back later.
Eventually, the user makes a purchase ("converts"). When the merchant
sends the confirmation page it includes a tracking pixel
(an invisible image) served off of the advertiser's site.
When the browser retrieves the pixel, it sends the advertiser's
cookie (1234) back to the advertiser. The cookie allows the
advertiser to connect
the original click and the resulting purchase, thus measuring the
conversion.
You'll note that what's technically being measured in this example is the conversion from the impression to the purchase. If you wanted to measure the click instead, there are a number of ways to do this, such as having the ad click redirect through the advertiser or having a Javascript hook that informed the advertiser of the click.
The problem with this technique is that it involves the advertiser tracking you across the Internet: it sees which Web site you are on every time it shows you an ad, and for a big ad network this can be a pretty appreciable fraction of your browsing history. This is a serious privacy problem and browsers are gradually deploying techniques to prevent this kind of tracking, such as Firefox's Enhanced Tracking Protection and Safari's Intelligent Tracking Protection. Those technologies are good for user privacy but interfere with conversion measurement. IPA is a mechanism designed to provide conversion measurement without degrading user privacy.
The Basic Idea #
The main idea behind IPA is to replace cookie-based linkage with
linkage based on an anonymous identifier. Let's assume that each client $i$
has a single unique identifier $I_i$ (I'll discuss how this identifier is
assigned below). This identifier can't be read directly
off the client but instead has to be accessed via an API
e.g., getIPAEvent() that produces an
encrypted version of the identifier $E(I_i)$.
The encryption is randomized so that each time the identifier is encrypted, the ciphertext is different,
preventing linkage of the encrypted identifiers. To represent that,
we use the notation $E(R_j, I_i)$ where $R_j$ is the randomizing
value. Two encrypted values $E(R_j, I_i)$ and $E(R_{j'}, I_{i'})$ will with high
probability be different unless both the identifier and the randomizer
are the same.
However, by use of an appropriate service they can be decrypted and matched up.
If we go back to the conversion scenario described above, but instead use IPA, it would look like this:
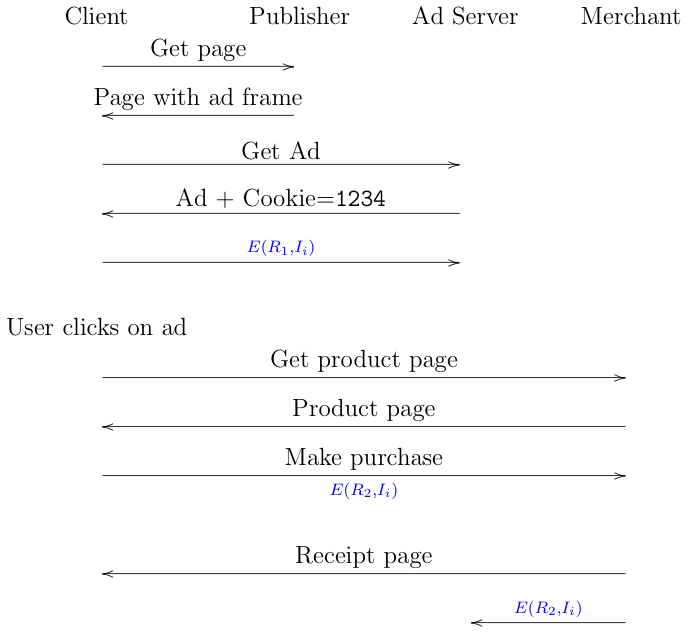
Everything is the same up to the point where the ad is displayed,
except that along with the ad the advertiser also sends some
Javascript code that calls getIPAEvent()[2]. The browser responds
by providing an encrypted version of the identifier, with
random value $R_1$: $E(R_1, I_i)$. The advertiser just stores
this information on a list of the impressions for this
ad (note that as before we are measuring impressions).
When the user actually buys the product, the merchant calls getIPAEvent()
and gets a new encrypted version of the identifier, this time with
a different randomizer,
$R_2$:
$E(R_2, I_i)$. The merchant sends the encrypted value it receives
to the advertiser. However, even though the identifiers are
the same, because the randomizers are different, the encrypted
values are different, thus preventing either the advertiser or the merchant from linking
them. The only thing that the advertiser knows is that there
has been one impression (because it saw it directly) and one
purchase (because the merchant told it about it). It's important
to note that this is all information that the merchant and the ad
server knew already: the only secret information is the identifier
and that's encrypted. In order to decrypt it and match up these
events, you need to use the IPA decryption and blinding service.
The basic idea behind the service is that the advertiser (or merchant) has a set of encrypted identifiers that it sends to the service and the service returns information about the number of matches. So, for instance, you might send in 20 encrypted identifiers and get back something like:
| Type | Count |
|---|---|
| Unmatched impressions | 2 |
| Unmatched purchases | 3 |
| Impression/purchase pairs | 6 |
| Two impressions/one purchase | 1 |
Note: it's important that the IPA service only operate on batches of reports and produce aggregate reports about the batch; otherwise the advertiser could just send in small numbers of reports at a time. More on this below.
Internally, the service works by having a pair of servers which cooperate to decrypt and blind the input values. The advertiser (or merchant) sends its values to the first server, which decrypts, blinds, and shuffles them, and then passes them on to the second server, which does the same thing, as shown in the diagram below (I've used a different color for each identifier to help make it easier to follow).

In this example, the advertiser has two encrypted impressions and two encrypted purchases (it knows which are which because that information was available when the API was called, so it can just label them). One of the impressions and one of the purchases line up but it doesn't know that. It passes all of its data in a batch to the first server of the IPA service (A) which partially decrypts them, blinds them with its secret, and then passes them to server B. Server B decrypts them the rest of the way and applies its own blinding key. At this point server B has a list of blinded identifiers labeled with whether they were impressions or purchases. Because the blinding keys are constant, each time identifier $I_1$ is blinded, the blinded values are the same, and so it can match up the impression and purchase for $I_1$ (both shown in blue). However, because the values are blinded, it can't match them up to the input reports. Given this information, the server it can then produce a report to the advertiser to the effect that there was one pair, one unmatched impression and one unmatched purchase.
Multi-Device #
One of the main requirements for the design of IPA is that it allow for linking activity across multiple devices. For instance, I might see an ad on my mobile device but make the purchase on my desktop machine. Obviously, advertisers and publishers want to be able to measure the impact of their ads. With the current cookie-based system it's possible under some circumstances to associate those events. For instance, if Facebook is displaying the ad and you're logged into Facebook, then your Facebook account ID can be used to link them up. A number of the proposed private conversion measurement systems (e.g., Apple's Private Click Measurement) do not allow for this use case, which is clearly a big part of Meta's motivation for proposing IPA, as a lot of their usage is on mobile.
IPA handles this case in a straightforward fashion, via the per-client identifier. Earlier I just assumed that each client $i$ had an identifier $I_i$ but didn't say how it was assigned. If instead, we arrange that each user has the same identifier across all of their devices, then IPA just naturally links up impressions on device A and device B without any extra work.
This of course reduces to the problem of how to get a per-user identifier synchronized across devices. One obvious approach would be to have the devices synchronize it, much as browsers can sync history across devices. However, there are a number of cases where this won't work, for instance if you use Chrome on your Android device and Firefox on your desktop,[3] or if the impression came from something other than a browser like an app or a smart TV (I'm no happier than you are about ads on my smart TV, let alone having their conversion measured).
IPA addresses this issue in a clever but counterintuitive fashion:
it allows any domain (e.g., example.com or more likely
facebook.com) to set a per-domain identifier (which IPA
calls a "match key") that
can be used by any domain. The idea here
is that when you log into some system (e.g., Facebook), it
sets an identifier that is tied to your account and is therefore
the same across all your devices. The identifier
can be used by any advertiser or merchant (via the getIPAEvent()
API), no matter which domain they are on, thus preventing
Facebook from being the only people who can do attribution
via the Facebook account.
Key to making this work is that the identifier is write-only: nobody—including the original domain—can access it, except by using the API, which of course only produces an unlinkable, encrypted value. This prevents the identifier from being used directly for tracking, as would otherwise be the case for a world-readable value. In fact, you can't even ask whether the identifier was set, because then it would leak one bit. Of course, the original domain knows the identifier for a given user (because it generated it) and it can set a cookie on the client to remember if it set the identifier, but if the cookie is deleted, then it doesn't know either.
IPA Technical Details #
This section provides technical details on how the IPA service works. I've attempted to make them mostly accessible and can be understood based on high school math[4] , but they can also be skipped if necessary. If you don't care about the details—or you already waded through this in my post on linking up vaccine doses—you can skip this section and still be fine.
Note: in ordinary integer math, given $g^a$ and $g$ it's easy to compute $a$ but we're going to be doing this in an elliptic curve where that computation is hard. Everything else is pretty much the same, but just remember that part.[5]
The service is implemented by having a pair of servers, $A$ and $B$. Each has a Diffie-Hellman key pair, which is to say a secret value $x$ and a public value computed as $g^x$. We'll call $A$'s key pair $(a, g^a)$ and $B$'s pair $(b, g^b)$. Each server also has a secret blinding key $K_a$ and $K_b$. These servers are operated by different entities who are trusted not to collude. However, if either service behaves correctly then you're OK. The service then publishes a combined public key $g^{a+b}$ which can be computed by multiplying the public keys: $g^a * g^b$ (if you remember your high school math!).
In order to submit an ID $I$, the sender first encrypts it. It generates a random secret $x$ and computes: $g^{x(a+b)} = {(g^{a+b})}^x$. Note that we're using the service combined public key and the sender's private value $x$, so the result is a secret from attackers who don't know either $x$ or $a+b$. It then multiplies $I$ by this value and sends the pair of values (this is just classic ElGamal Encryption, but to the key $g^{a+b}$):
$$g^x, I * g^{x(a+b)}$$
Importantly, this second term can be broken up into a part involving only $a$ and a part involving only $b$. I.e.,
$$I * g^{x(a+b)} = I * g^{xa} * g^{xb}$$
Again, this is just high school math. These values then get sent to $A$ (or $B$, it doesn't matter), who computes $g^{xa} = {(g^{x})}^a$ (recall it knows $a$). It then divides the second part by $g^{xa}$:
$$I *g^{xb} = \frac{I * \cancel{g^{xa}} * g^{xb}}{\cancel{g^{xa}}}$$
This cancels out the $g^{xa}$ term, leaving you with just a term that involves $b$, and thus the pair:
$$g^x, I * g^{xb}$$
$A$ then blinds this value, by exponentiating both values to $K_a$, giving:
$$(g^x)^{K_a}, (I * g^{xb})^{K_a}$$
We can flatten this out to give:
$$g^{x * K_a}, I^{K_a} * g^{(xb)(K_a)}$$
$A$ batches these values up with other inputs it has received, shuffles them, and sends them to $B$. $B$ takes the first term and computes $(g^{x*Ka})^b = g^{x * K_a * b} = g^{(xb)(K_a)}$. It then divides the second term by this value, to get:
$$I^{K_a} = \frac{I^{K_a} * \cancel{g^{(xb)(K_a)}}}{\cancel{g^{(xb)(K_a)}}}$$
Finally, $B$ blinds the value by taking it to the power $K_b$, this giving us:
$$I^{(K_a)(K_b)} = (I^{K_a})^{K_b}$$
That was a lot of math, but the bottom line is that the actual
identifier $I$ (e.g., the SSN -- Updated 2022-02-16 account id) has been
converted into a new blinded value, with (hopefully) the following properties:
- Neither $A$ or $B$ ever saw $I$
- $A$ sees the input encrypted version but doesn't learn the blinded version.
- $B$ sees the blinded version but doesn't learn the encrypted version.
- You need to know $K_a$ and $K_b$ to compute the blinded version of $I$.
Disclaimer: The IPA documents were just published recently, so I don't think they have seen enough analysis to prove they are secure. Here I'm just describing how it's supposed to work.
Privacy Properties #
The basic two privacy properties we are trying to achieve here are:
-
Neither the advertiser nor the merchant is able to associate a specific input report to a specific output report, even with the help of one of the servers (because you need both $K_a$ and $K_b$). This is true even if they also know the identifiers, which are not even required to be high entropy (e.g., they can be e-mail addresses).
-
Neither the advertiser nor the merchant is able to determine which users are represented in a given set of reports or are associated with a given piece of additional data (see below).
As far as I know, no attacks on property (1) are known (though see the above caveat about insufficient analysis) but we do know of an attack on property (2) (see the appendix). The basic situation is that the advertiser can collude with whoever issued the match keys and with one of the servers to determine if a given user is incorporated in a set of reports. However, if both servers are honest, this attack will not work. This is not the desired privacy target, which is that you only have to trust that at least one server is honest, but it's where things currently stand.
In any case, the second server learns more than the first server because it knows which reports match up with which other reports. However, it still doesn't know which ones match up to which input reports because it doesn't know $K_a$. This is still a somewhat weird asymmetry, and when we look at additional data in the next section, we'll remove it.
Importantly, the summaries that are provided to the advertiser can still leak data. For instance, suppose that the advertiser wants to know if impression A and purchase B are from the same user: it can send them in together with a bunch of fake reports which have random non-matching identifiers. If the report that comes back lists any matches, then it know that A and B match. This is a generalized problem in any aggregate reporting system which I covered in some detail previously and there are a variety of potential defenses, including trying to ensure that data comes from "valid" clients and adding noise to the output. The IPA proposal contemplates some kind of noise injection along with budgeting for the number of queries but doesn't really include a complete design.
Although this system provides a fair degree of privacy if you trust the servers, there will of course be people who don't trust them, or just don't want to send their data on principle. One question I've seen asked is whether it will be possible to configure your software not to participate. However, from a privacy perspective, it's actually undesirable to have the API call just fail because then you have sent some information to the server that might be used to track you (as most people will not disable the API). A better approach technically is just to send an unusable report, e.g., the encryption of a randomly selected ID. This should not be possible to distinguish from a valid report without the cooperation of both servers and knowing what valid identifiers look like. Obviously, whether there is such a configuration knob depends on the software you are using.
Additional Data #
So far the system we have described just lets us count matches, but what if we want to record more than matches, for instance by measuring the total amount of money spent by customers via a given ad campaign? This turns out to be a somewhat tricky problem to solve because we need to make sure that that information doesn't turn into a mechanism for tracking reports through the system.
For instance, in the diagram above, I had the advertiser label each report as either an impression or a purchase; this is mostly fine as long as we only have those two labels because if there are a reasonable number of each you don't know much about whether a given output and a given input match up. However, if we let the advertiser attach arbitrary labels, this would obviously be a problem because then they could collude with one of the servers to track a given input through the process (this is of course the same reason you have to shuffle). Naively, suppose that the merchant adds the customer's email address to the report, then obviously if that pops out the other end then you have a real problem.
IPA doesn't contain a complete proposal for this, but does have some handwaving. The general idea is that the client, not the advertiser or merchant would attach "additional data" (the cute name for this is a "sidecar") to their report. This data would be supplied by the server which would say something like "make a report that says that this purchase was for 100 dollars". This additional data would also be multiply encrypted so that neither server could individually decrypt it, but that once it had been shuffled, the second server would get it along with the blinded identifier. Note that this additional data would not be blinded because otherwise you wouldn't be able to add up the results; it just appears unmodified in the output.
But wait, you say, if we just let the advertiser provide arbitrary data, then it can provide a user identifier of its own which will then show up in the output and we're back where we started. The proposed fix is that instead of just reporting the value directly, the client instead reports it via some secret-sharing mechanism like Prio. Of course, this means that the client actually has to submit two reports, one that is processed by server A then server B and one that is processed by server B then server A, as shown below:

As shown here, the client generates two reports, each of which contains a Prio share for the value provided by the advertiser. When the advertiser is ready, it sends one report share to Server A and one report share to Server B. In this case, I've shown reports from two clients, each with one share. As described above, each server partly decrypts its reports, shuffles, and then passes it to the other server. The other server completes the decryption, correlates the matching reports, and aggregates (e.g., adds up) the additional data.[6] Finally, Server A sends its aggregated additional data to Server B which combines it with its aggregated additional data and sends the result back to the advertiser (see my post on Prio for more details on how this part of the process works).
So far so good, except that I haven't specified how the additional data is encrypted. This part turns out to be somewhat tricky and the IPA authors don't have a published design for it at the moment, so this is piece is still a hard hat area.
Status of IPA #
So what's the status of IPA? This has been the source of some confusion, perhaps in part because Google has implemented some of their "Privacy Sandbox" proposals in Chrome and has already done or proposed to do "origin trials" (a kind of limited access test) for them. At present, however, IPA is just a proposal. It has been submitted to the W3C Private Advertising Technology Community Group for consideration but has yet to be adopted, let alone shipped by anyone. In other words, it's a potentially interesting idea but not something that is finished or ready to standardize.
Appendix: Linear Relation Attacks #
The IPA authors describe a few known attacks on the system (though more analysis is needed). The most interesting one is what they term "linear relation" attacks. The basic idea behind this kind of attack is to use the blinding process as an oracle to determine whether a given user was in the report set.
Recall that the result of the blinding process for identity $I_i$ is $I_i^{K_a K_b}$. So if you have two identities $I_1$ and $I_2$ their blinded versions are of course: $I_1^{K_a K_b}$ and $I_1^{K_a K_b}$,
These have the interesting property that:
$$(I_1^{K_a K_b})(I_2^{K_a K_b}) = (I_1 I_2)^{K_a K_b}$$
Updated 2022-02-16: oops, fixed a subscript
If the advertiser knows a user's identifier and it has the cooperation of one of the servers, it can use this fact to determine whether a given user was in a set of reports. If the target user has identifier $I_t$ it creates two fake reports $I_x$ and $I_y$ such that: $I_y = I_tI_x$. When these are blinded, the result is:
- $I_x^{K_a K_b}$
- $I_y^{K_a K_b} = (I_x I_t)^{K_a K_b} = (I_x^{K_a K_b})(I_t^{K_a K_b})$
And if a report from the target was included, then the reports will also included the blinded version of $I_t$, which is $I_t^{K_a K_b}$.
The colluding server then looks to see whether there are a triplet of blinded values $(B_1, B_2, B_3)$ such that $B_1 = B_2 * B_3$. If there are, then they know that $B_1$ corresponds to $I_y$ and that one of $B_2$ or $B_3$ corresponds to $I_t$.[7] As I said above, this is a known attack and the authors are working on ideas to address it. Note also that this attack depends on knowing users identifiers, so it can't be done by any site, but just by (or with the help of) the one issuing the identifiers.
Usually this is from an ad network of some kind, but I'm simplifying. ↩︎
The actual proposal proposal uses different names for the impression and the purchase, but that's not necessary for this simple example. ↩︎
Yes, it's bad that sync between browsers of different manufacturers doesn't work, but that's a whole different story. ↩︎
In particular, the facts that $(g^a)(g^b) = g^{a+b}$ and $(g^a)^b = g^{ab}$. ↩︎
Yes, I know I'm using exponential notation. It's easier to follow for people not used to EC notation. ↩︎
I've omitted the discussion of the Prio proofs for simplicity. ↩︎
Note that another way to execute this is to just create a new identity that is the product of two existing identities; this lets you learn if both are in a set of reports. ↩︎