Maybe someday we'll actually be able to search the Web privately
A look at the new Tiptoe encrypted search system
Posted by ekr on 02 Oct 2023

The privacy of Web search is tragically bad. For those of you who haven't thought about it, the way that search works is that your query (i.e., whatever you typed in the URL bar) is sent to the search engine, which responds with a search results page (SERP) containing the engine's results. The result is that the search engine gets to learn everything you search for. The privacy risks here should be obvious because people routinely type sensitive queries into their search engine (e.g., "what is this rash?", "Why do I sweat so much", or even "Dismemberment and the best ways to dispose of a body)", and you're really just trusting the search engine not to reveal your browsing history.
In addition to learning about your search query itself, browsers and search engines offer a feature called "search suggestions" in which the search engine tries to guess what you are looking for from the beginning of your query. The way this works is that as you start typing stuff into the search bar, the browser sends the characters typed so far to the search engine, which responds with things it thinks you might be interested in searching for. For instance, if I type the letter "f" into Firefox, this is what I get:
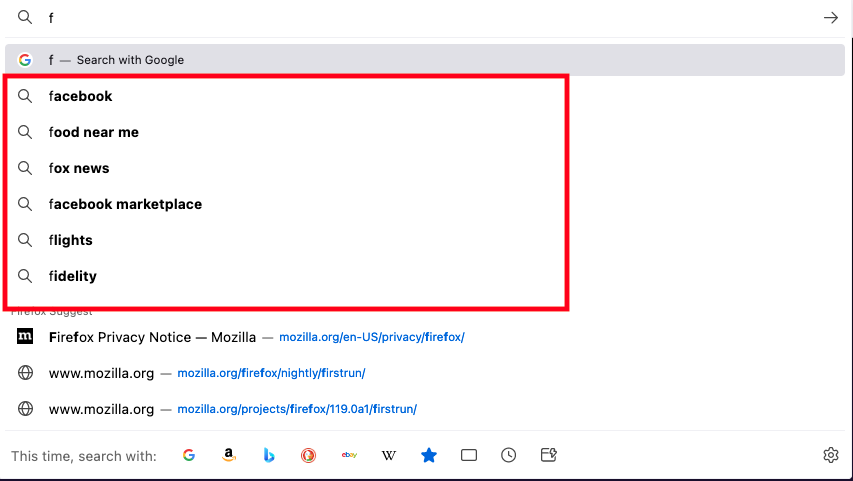
Everything in the red box is a search suggestion from Google. The stuff below that is from a Firefox-specific mechanism called Firefox Suggest which searches your history or—depending on your settings—might ask Mozilla's servers for suggestions. The important thing to realize here is that anything you type into the search bar might get sent to the server for autocompletion, which means that even in situations where you are obviously just typing the name of a site, as in "facebook"[1]
Your privacy in this setting basically consists of trusting the search engine; even if the search engine has a relatively good privacy policy, this is still an uncomfortable position. Note that while Firefox and Safari—but not Chrome!—have a lot of anti-tracking features, they don't do much about this risk because they are oriented towards ad networks tracking you cross sites, but all of this interaction is with a single site (e.g., Google.) There are some mechanisms for protecting your privacy in this situation—primarily concealing your IP address—but they're clunky, generally not available for free, and require trusting some third party to conceal your identity.
This situation is well-known to most people who work on browsers—and to pretty much anyone who thinks about it for a minute—of course you have to send your search queries to the search engine, if it doesn't have your query, it can't fulfill your request. But what if it could?
This is the question raised by a really cool new paper by Henzinger, Dauterman, Corrigan-Gibbs, and Zeldovich about an encrypted search system called "Tiptoe".[2] Tiptoe promises fully private (in the sense that the server learns nothing about what you are searching for) search for the low low price of 56.9 MiB of communication and 145 core-seconds of server compute time. Let's take a look.
Background: Embeddings #
In order to understand how Tiptoe works, we need some background on what's called an embedding. The basic idea behind an embedding is that you can take a piece of content such as a document or image and convert it into a short(er) vector of numbers that preserves most of the semantic (meaningful) properties of the input. They key property here is that two similar inputs will have similar embedding vectors.
As an intuition pump, consider what would happen if we were to simply count the number of times the 500 most common English language words appear in the text. For example, look at this sentence:
I went to the store with my mother
This contains the following words from the top 500 list (the numbers in parentheses are the appearance on the list with 0 being the most common):
- the(0)
- to(2)
- with(12)
- my(41)
- went(327)
We can turn this into a vector of numbers by just making a list where each entry is the number of times the corresponding word is present, so in this case it's a vector of 500 components (dimension 500), as in:
1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
That's a lot of zeroes, so let's stick to the following form which lists the words that are present:
[the(0) to(2) with(12) my(41) went(327)]
Let's consider a few more sentences:
| Number | Sentence | Embedding |
|---|---|---|
| 1 | I went to the store with my mother | [the(0) to(2) with(12) my(41) went(327)] |
| 2 | I went to the store with my sister | [the(0) to(2) with(12) my(41) went(327)] |
| 3 | I went to the store with your sister | [the(0) to(2) with(12) your(23) went(327)] |
| 4 | I am going to create the website | [the(0) to(2) going(140) am(157) website(321) create(345)] |
As you can see, sentences 1 and 2 have exactly the same embedding, whereas sentence 3 has a similar but not identical embedding, because I went with your sister rather than with my (mother, sister). This nicely illustrates several key points about embeddings, namely that (1) similar inputs have similar embeddings and (2) that embeddings necessarily destroy some information (technically term: they are lossy). In this case, you'll notice that they have also destroyed the information about where I went with (your, my) (mother, sister, friend). By contrast, sentence (4) is a totally different sentence and has a much smaller overlap, consisting of only the two common words "the" and "to"[3]
Once we have computed an embedding, we can easily use it to assess how similar two sentences are. One conventional procedure (and the one we'll be using for the rest of this post) is to instead take what's called the inner product of the two vectors, which means that you take the sum of the pairwise product of the corresponding values in each vector (i.e., we multiply component 1 in vector 1 times component 1 in vector 2, component 2 times component 2, and so on). I.e.,
$$ P = \sum_i V_1[i] * V_2[i] $$
The way this works is that we start by looking at the most common word ("the"). Each sentence has one "the", so that component is one in each vector. We multiply them to get 1. We then move on to the second most common English word (which happens to be "and"). Neither sentence has "and", so in both vectors this is a 0, and 0*0 = 0. Next we look at the third-most common word ("to"), and so on. We can draw this like so, for the inner product of S1 and S2.
$$ \begin{matrix} the \\ and \\ to \\ ... \\ with \\ ... \\ my \\ .... \\ went \\ \end{matrix} \begin{bmatrix} 1 \\ 0 \\ 1 \\ ... \\ 1 \\ ... \\ 1 \\ ... \\ 1 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \\ 1 \\ ... \\ 1 \\ ... \\ 1 \\ ... \\ 1 \\ \end{bmatrix} = (1 + 1 + 1 + 1 + 1) = 5 $$
By contrast, if we take S1 and S3 we get:
$$ \begin{matrix} the \\ and \\ to \\ ... \\ with \\ ... \\ your \\ ... \\ my \\ .... \\ went \\ \end{matrix} \begin{bmatrix} 1 \\ 0 \\ 1 \\ ... \\ 1 \\ ... \\ 0 \\ ... \\ 1 \\ ... \\ 1 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \\ 1 \\ ... \\ 1 \\ ... \\ 1 \\ ... \\ 0 \\ ... \\ 1 \\ \end{bmatrix} = (1 + 1 + 1 + 0 + 0 + 1) = 4 $$
This value is lower because one sentence has "your" and the other has "my" but neither has both "your" and "my". Finally, if we take S1 and S4, we get:
$$ \begin{matrix} the \\ and \\ to \\ ... \\ with \\ ... \\ my \\ .... \\ went \\ \end{matrix} \begin{bmatrix} 1 \\ 0 \\ 1 \\ ... \\ 1 \\ ... \\ 1 \\ ... \\ 1 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \\ 1 \\ ... \\ 0 \\ ... \\ 0 \\ ... \\ 0 \\ \end{bmatrix} = (1 + 1 + 0 + 0 + 0) = 3 $$
What you should be noticing here is that the more similar (the more words they have in common) the embedding vectors are, the higher the inner product. The conventional interpretation is that each embedding vector represents a d-dimensional vector where n is the number of components and that the closer the angle between the two vectors (the more the point in the same direction) the more similar they are. Conveniently, the inner product is equal to the cosine of the angle, which is 1 when the angle is 0 and 0 when the angle is 90 degrees, and so can be used as a measure of vector similarity. Personally, I don't think well in hundreds of dimensions so I've never found this interpretation as helpful as one might like, but maybe you will find it more intuitive, and it's good to know anyway.
Normalization #
I've cheated a little bit in the way I constructed these sentences, because using this definition sentences which have more of the common English words (e.g., longer sentences) will tend to look more similar than those which do not. For instance, if instead I had used the sentences:
S5: I have been to the store with my sister
S6: I have been to the store with your sister
| Number | Sentence | Embedding |
|---|---|---|
| 2 | I went to the store with my mother | [the(0) to(2) with(12) my(41) went(327)] |
| 5 | I have been to the store with my sister | [the(0) to(2) with(12) have(19) my(41) been(60)] |
| 6 | I have been to the store with your sister | [the(0) to(2) with(12) have(19) your(23) been(60)] |
You'll notice that sentences 2 and 5 have four words in common (the, to, with, my), whereas 5 and 6 have five words in common (the, to, with, have, been), even though they (at least arguably) have quite a different meaning (who I went to the store with) rather than just differing in grammatical tense (have been versus went).
The standard way to fix this is to normalize the vectors so that the the larger the values of components in aggregate, the less the value of each individual component matters. For mathematical reasons, this is done by setting magnitude of the vector (the square root of the sum of the squares of each component) to 1, which you can do by dividing each component by the magnitude. When we do this, we get the following result:
| Sentence Pair | Un-normalized Inner Product | Normalized Inner Product |
|---|---|---|
| S2 and S5 | 4 | 0.73 |
| S2 and S6 | 5 | 0.55 |
This matches our intuition that sentences 2 and 5 are more similar than sentences 2 and 6.

Real-world Embeddings #
Obviously, I'm massively oversimplifying here and in the real world an embedding would be a lot fancier than just counting common words. Typically embeddings are computed using some fancier algorithm like Word2vec, which itself might use a neural network. However, the cool thing here is that however you compute the embedding, you can still compute the similarity of two embeddings in the same way, which means that you can just build a system that depends on having some embedding mechanism and then work out that embedding separately. This is very convenient for a system like Tiptoe where we can just assume there is an embedding and work out cryptography that will work generically for any embedding.
Tiptoe #
With this background in mind, we are ready to take a look at Tiptoe.
Naive Embedding Based Search #
Let's start by looking at how you could use embeddings to build a search engine. The basic intuition here is simple. You have a corpus of documents (e.g., Web pages) $D_1, D_2 ... D_n$. For each document, you compute a corresponding embedding for the document $Embed(D_1), Embed(D_2), ... Embed(D_n)$. When the user sends in their search query $Q$ you compute $Embed(Q)$ and return the document(s) that are closest to $Embed(Q)$, which is to say have the highest inner products.[4] Naively, you just compute the inner product of the embedded query against every document embedding and then take the top values, though of course there are more efficient algorithms.
The figure below shows a trivial example. In this case, the client's embedded query is most similar to $Embed(D_4)$, and so the server sends $D_4$ (or, in the case of search, its URL) in response.
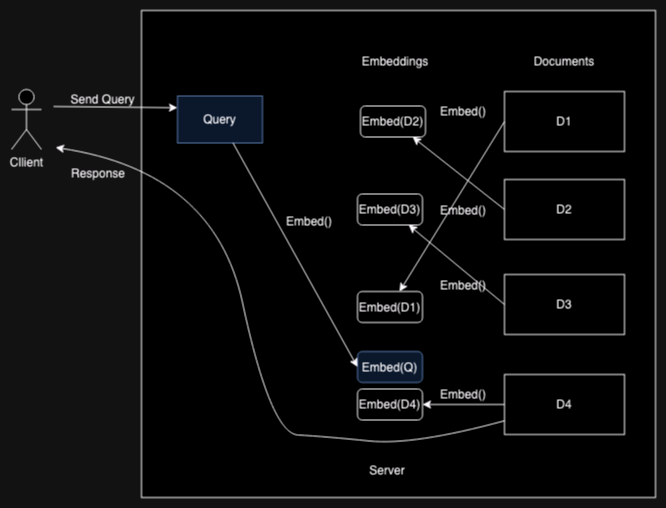
This is actually a very simplified version of how modern systems such as ColBERT work.
Of course the problem with this system is the same as the problem we started with, because you have to send your query to the server so it can compute the embedding. There are two obvious ways to address this:
- Compute the embedding on the client and send it to the server.
- Send the entire database to the client
The first of these doesn't work because the embedding contains lots of information about the query (otherwise the search engine couldn't do its job). The second doesn't work because the embedding database is far too big to send to the client. What we need is a way to do this same computation on the server without sending the client's cleartext query or its embedding to the server.
Naive Tiptoe: Inner Products with Homomorphic Encryption #
Tiptoe addresses this problem by splitting it up into two pieces. First, the client uses a homomorphic encryption encryption system to get the server to compute the inner product for each document without allowing the server to see the query.
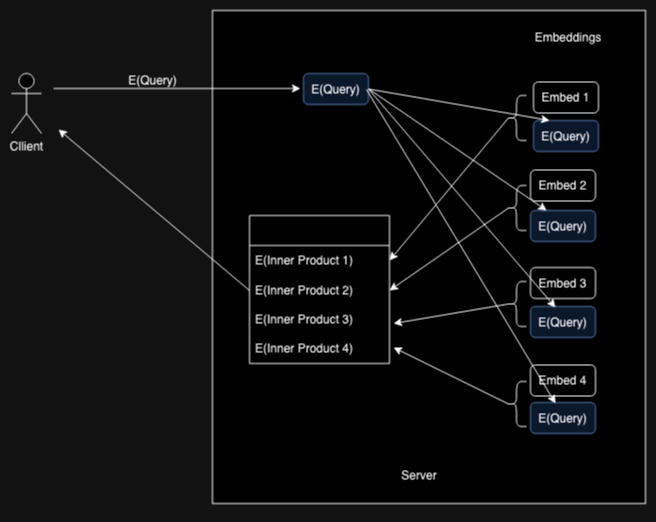
The client then ranks each results by its inner product, which gives
it a list of the results that are most relevant (e.g., results 1, 3, 9).
The indices themselves aren't useful: the client needs the URL
for each result, so it uses a Private Information Retrieval (PIR) scheme to retrieve
the URLs associated with the top results from the server.
The reason for this two-stage design is that the URLs themselves are fairly large, and so having the server provide the URL for each result is inefficient, as most of the results will be ranked low and so the user will never see them. The server can also embed the type of preview metainformation that typically appears on the SERP (e.g., a text snippet) if it wanted to, but because PIR is expensive, you want the results to be as small as possible. Once the client has the URLs, the it can just go directly to whichever site the user selects.
I already explained PIR in a previous post, so this post will just focus on the ranking system. This system uses some similar concepts to PIR, so you may also want to go review that post. You may recall from that post that a homomorphic encryption scheme is one in which you can operate on encrypted data. Specifically, if you have two plaintext messages $M_1$ and $M_2$ and their corresponding ciphertexts $E(M_1)$ and $E(M_2)$ then the encryption is homomorphic with respect to a function $F$ if
$$ F(E(M_1), E(M_2)) = E(F(M_1, M_2)) $$
So, for instance, if you were to have an encryption function which is homomorphic with respect to addition, that would mean you could add up the ciphertexts and the result would be the encryption of the sum of the plaintexts. I.e.,
$$ E(A) + E(B) = E(A + B) $$
Homomorphic encryption allows you to give some encrypted values to another party, have it operate on them and give you the result, and then you can decrypt it to get the same result as if they had just operated on the plaintext values, but without them learning anything about the values they are operating on.
We can apply homomorphic encryption to this problem as follows. First, the client computes the embedding of the query giving it an embedding vector $V$ and each element of it $i$, $V_i$. The client then encrypts each element of $V$ with a homomorphic encryption system. Call this $E(V)$ and each element $E(V_i)$. The client sends $E(V)$ to the server.
The server iterates over each URL $U_j$ and its corresponding embedding value $D_j$ and computes the inner product of $D_j$ and $E(V)$. Specifically, for each element $i$, it computes the pairwise product $I_{j, i}$:
$$ E(I_{j,i}) = D_{j,i} * E(V_i) $$
It then sums up all these values, to get the encrypted inner product for URL $j$.
$$
E(I_j) = \sum_i E(IP_{j,i}) = \begin{matrix}E(V_1 * D_1) \\
+ \\
E(V_2 * D_2) \\
+ \\
E(V_3 * D_3) \\
+ \\
E(V_4 * D_4) \\
+ \\
E(V_5 * D_5)
\end{matrix}
$$
Written in pseudo-matrix notation, we get:
$$ \begin{bmatrix} E(V_1) \\ E(V_2) \\ E(V_3) \\ E(V_4) \\ E(V_5) \\ \end{bmatrix} \cdot \begin{bmatrix} D_1 \\ D_2 \\ D_3 \\ D_4 \\ D_5 \\ \end{bmatrix} \rightarrow \begin{bmatrix} E(V_1 * D_1) \\ E(V_2 * D_2) \\ E(V_3 * D_3) \\ E(V_4 * D_4) \\ E(V_5 * D_5) \\ \end{bmatrix} \rightarrow \sum_i E(V_i * D_i) $$
The server then sends back the encrypted inner product values to the client (one per document in the corpus). The client decrypts them to recover the inner product values (again, one per document). It can then just pick the highest ones which are the best matches and retrieve their URLs via PIR (effectively, "give me the URLs for documents 1, 3, 9", etc.). It then dereferences the URLs as normal. Because this is all done under encryption, the server never learns your search query, the matching documents, or the URLs you eventually decide to dereference (though of course those servers see when you visit them). Importantly, these guarantees are cryptographic, so you don't have to trust the server or anyone else not to cheat. This is different form proxying systems, where the proxy and the server can collude to link up your searches and your identity.
Ciphertext Size Matters #
For instance:
-
If each value in the embedding vector is a 32-bit floating point number and the embedding vector has dimension 700ish, then the embedding values for each document is around 2800 bits.
-
If we naively use ElGamal encryption, then each ciphertext will be around 64 bytes (480 bits).
This is an improvement of a factor of 7 or so, but at the cost of doing $N$ encryption operations, which is quite a lot.
Clustering #
Let's take stock of where we are now. The client sends a relatively short value, consisting of $T$ ciphertexts where $T$ is the number elements in the embedding vector. The server responds with $N$ ciphertexts, where $N$ is the number of URLs in its corpus and has to do $T*N$ multiplications. Depending on the homomorphic encryption algorithm, this might or might not be an improvement on the total communication bandwidth, but it's still linear in the number of documents, which is quite bad.
It's not really possible to reduce the number of operations on the server below linear. The reason for this is that the server needs to operate on the embedding for each document; otherwise the server could determine which embeddings the client isn't interested in by which ones it doesn't have to look at it in order to satisfy the client's query. However, it is possible to significantly improve the amount of bandwidth consumed by the server's response.
The trick here is that the server breaks up the corpus of documents into clusters of approximately $\sqrt N$ size (hence there are approximately $\sqrt N$ clusters). These clusters are arranged so that they have nearby embedding vectors, and hence the documents are are theoretically similar. The server publishes the embedding vector for the center of the cluster, and this allows the client to request only the inner products for the closest cluster. This reduces the amount of data that the server by a factor of $\sqrt N$ to order $\sqrt N$. There's just one problem: if the client only queries one cluster, then doesn't the server know which cluster the client is interested in?
We fix this by having the client send a separate encrypted query for each cluster, like so:
$$ \begin{bmatrix} E(0) & \color{red}{E(V_1)} & E(0) \\ E(0) & \color{red}{E(V_2)} & E(0) \\ E(0) & \color{red}{E(V_3)} & E(0) \\ E(0) & \color{red}{E(V_4)} & E(0) \\ E(0) & \color{red}{E(V_5)} & E(0) \\ \end{bmatrix} $$
In this diagram, each column represents one cluster (and hence there are $\sqrt N$ columns), and each row is a different embedding component. The column corresponding to the cluster (column $q$) of interest (in red) contains the encryption of the client's actual query embedding vector, whereas the rest of the columns just contain the encryption of 0 (the encryption is randomized so that they are not readily identifiable).
The server takes each column of the client's query and computes the inner product for each document the corresponding cluster, as before. I.e., for document $j$ in cluster $c$, it computes $E(I_{c, j})$. Then, however, the server adds up the inner product values across the clusters, with one report for the the sum of the values for 1st URL in each cluster, one for the the sum of the inner products for the 2nd URL, and the cluster, and so on, so that the server still only returns the same number of of ciphertexts as before. I.e., it reports:
$$ E(I_j) = \sum_c E(I_{c, j}) $$
Ordinarily the sum of these would be useless, but the trick[5] here is that because the other columns—corresponding to the cluster that is not of interest—are the encryption of 0, their inner products are also zero, which means that the result sent back to the client only includes the inner products for the column of interest (column $q$).
The resulting scheme has much better communication overhead:
- The server sends the list of the centers of the embeddings ($\sqrt N$).
- The client sends a list of $d$ encrypted components for each cluster ($d \sqrt N$).
- The server sends a single encrypted inner product value for each document in the cluster ($\sqrt N$).
This is dramatically better than the naive scheme in which the client sends $d$ values and the server sends $N$, although at the cost of pushing some of the transmission cost onto the client, for a total transmission that scales as a factor of $(d+2)\sqrt N$. Of course, that's still pretty big and the constant factor is also pretty big (~512 bits per document for ElGamal). The Tiptoe paper uses some clever tricks to bring the size down some (see below for cost numbers) but the end result is still fairly large (see cost below).
Performance #
As should be clear from the previous section it's possible to build privacy-preserving search, but how well does it actually do? This actually comes down to two questions:
- How good are the answers?
- How much does it cost?
Accuracy #
First, let's take a look at accuracy. Obviously, a private search mechanism will be no better than a non private search mechanism, because if it were you could just remove the privacy pieces and get the same accuracy. However, realistically we should expect worse accuracy, just on general principle (i.e., we are hiding information from the server). In this specific case we should expect worse accuracy because the server is just operating on the (encrypted) embedding of the query, rather than the whole query, and computing the embedding destroys some information.
The metric the authors use for performance is something called "MRR@100", which stands for "mean reciprocal rank at 100". The way this works is that for each query you determine which result people would have ranked at number 1 and then ask what position the search algorithm returned it in. You then compute a score that is the inverse of that position, so, for instance, if the document were found in position 5, then the score would be $1/5$. The "mean" part is that you average out the results over the document corpus. The "at 100" part is that if the search algorithm doesn't return the result in the top 100 values, you get a score of zero. In other words:
$$ MRR = \frac{\sum_i^N \begin{cases} \frac{1}{Rank_i} & \text{if } R_i \leq 100 \\ 0 &\text{otherwise} \end{cases} } {N} $$
Note that this score really rewards getting the top result, because even getting it in second place only gets you a per-document score of $1/2$.
The results look like this:
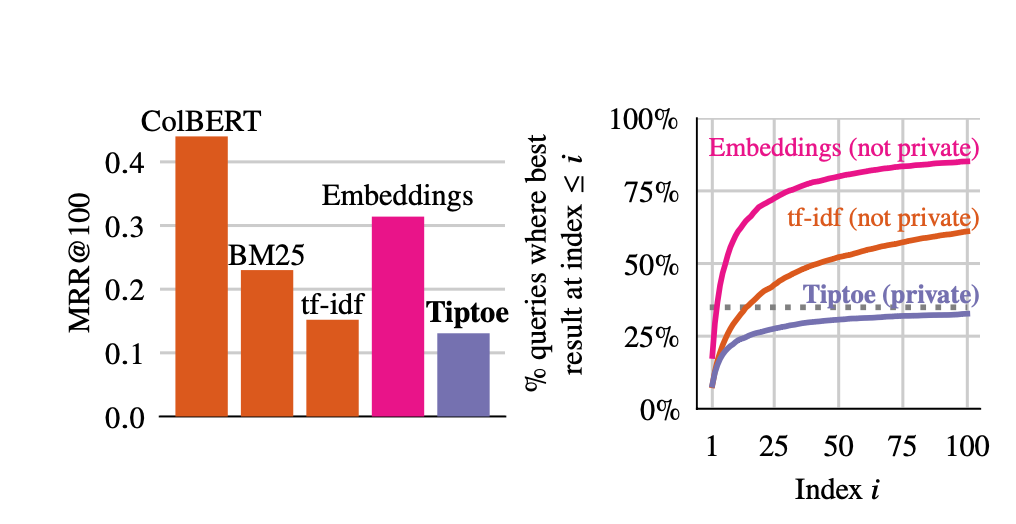
The graph on the left provides MRR@100 comparisons to a number of algorithms, including:
- A modern search algorithm (ColBERT)
- Two somewhat older systems (BM25 and tf-idf)
As you can see, ColBERT performs the best and Tiptoe gets pretty close to tf-idf but is still significantly worse than BM-25. The "embeddings" is the result if you don't use the clustering trick described above. Notice here that "embeddings" does very well, and in fact is better than BM25, so the clustering really does have quite a significant impact on the quality of the results.
The graph on the right shows the cumulative probability that the best result will be found at an index less than $i$ (i.e., that it is found in the top $i$ results). The dotted line shows the chance that the best result is in the cluster Tiptoe receives at all; which reflects the best result Tiptoe could deliver even if it always picked the best result out of the cluster (about 1/3 of the time).
On the one hand, this is a fairly large regression from the state of the art, but on the other hand, it means that there is a lot of room for improvement just by improving the clustering algorithm on the server. Obviously, there's also room for improvement in terms of ranking within the cluster. With the current design the client just gets the inner product so all it can do is rank them, but there might be some things you could do, such as proactively retrieving the first 10 documents or so (there is a very steep improvement curve within the first 10) and running some local ranking algorithm on their content.
Cost #
So how much will all this cost. The answer is "quite a bit but not as much as you would think". Here's Figure 8, which shows the estimated cost of Tiptoe for various document sizes:
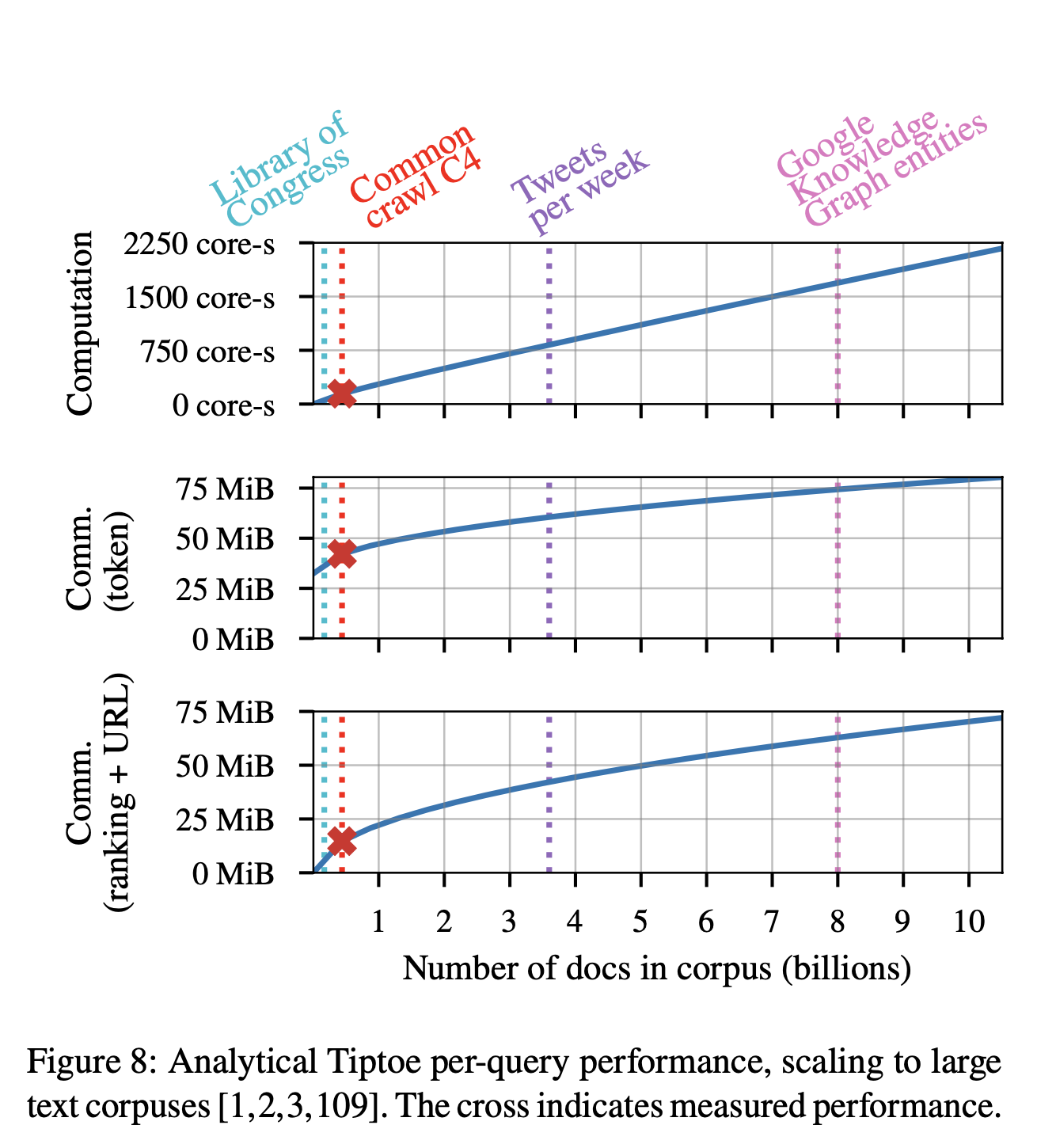
The server CPU cost is linear in the number of documents in the corpus and would require around 1500 core seconds for something like Google.
The communication cost is sublinear in the number of documents but has a very high fixed cost of around 55 MiB for a query on a corpus the size of the Common Crawl data set (~360 million documents) and around 125 MiB for a Google sized system (~8 billion documents). Tiptoe uses a number of tricks to frontload this cost; most of the communication isn't dependent on the query, so that the client and server can exchange it in advance without it being in the critical path. The server also has to send the client the embedding algorithm, which can be quite large (e.g, 200+ MiB) but that is reused for multiple queries and so can be amortized out.
Using Amazon's list price costs, the overall cost is around 0.10 USD/query for a system the size of Google. Google doesn't publish their numbers but 9to5Google estimates it at .002 USD/query. This is 50 times less, which is a big difference, but actually that probably overstates the difference because Google isn't paying list price for their compute costs, so the difference is probably quite a bit less. In either case, this is actually a smaller difference than you would expect given the enormous improvement in privacy.
The Bigger Picture #
The lesson you should be taking home here is not that Tiptoe is going to replace Google search tomorrow. Not only are private search techniques like this more expensive than non-private techniques, they are inherently less flexible. Google's SERP is a lot more than just a list of results. For instance here's the top of the search page for "tiptoe":
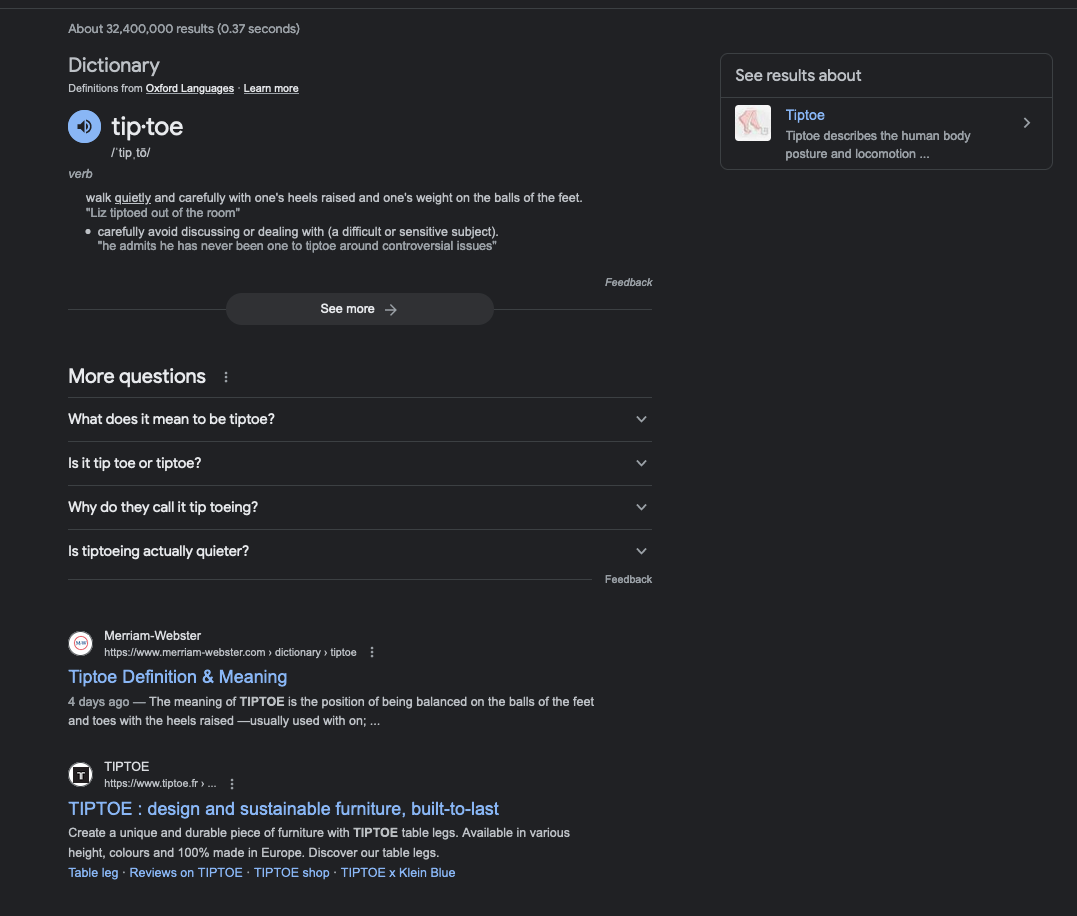
Note that the first entry is actually a dictionary definition, the info-box on the right, and the alternate questions. The first website result is below all that. Obviously, one could imagine enhancing a system like Tiptoe to provide at least some of these features, though at yet more cost.
There are two stories here that are true at the same time. The first is about technical capabilities: in most cases, private systems are inherently less flexible and powerful than their non-flexible counterparts. It's always easier to just tell the server everything and let it sort out what to do, both because the server can just unilaterally add new features without any help from the client and because it's often difficult to figure out how to provide a feature privately (just look at all the fancy cryptography that's required to provide a simple list of prioritized URLs). This will almost always be true, with the only real exception being cases where the data is so sensitive that it's simply unacceptable to send it to the server at all, and so private mechanisms are the only way to go. However, I think the lesson of the past 20 years is that people are actually quite willing to tell their deepest secrets to some computer, so those cases are quite rare.
The other story is about path dependence. Google search didn't get this fancy at all once; the original search page was much simpler (basically a list of URLs with a snippet from the page) and features were added over time. If we imagine a world in which privacy had been prioritized right from the start, then we would have a much richer private search ecosystem—though most likely not as powerful as the one we have now. The entry barrier to increased data collection for slightly better features would most likely be a lot higher than it is today. But because we started out with a design that wasn't private, it led us naturally to where we are today, where every keystroke you type in the URL/search bar just gets fed to the search provider.
I'm not under any illusions that it will be easy to reverse course here: even in the much simpler situation of protecting your Web traffic in transit, it's taken decades to get out from under the weight of the early decisions to do almost everything in the clear and we're still not completely done. Moreover, that was a situation where we had the technology to do it for a long time, and it was just a matter of deployment and cost. However, the first step to actually changing things is knowing how to do it, and so it's really exciting to see people taking up the challenge.
Acknowledgement #
Thanks to Henry Corrigan-Gibbs for assistance with this post. All mistakes are of course mine.
Firefox, at least, does make some attempt to omit pure navigational queries, so if you type "http://" in the Firefox search box, this gets sent to the server, but "http://f" does not. ↩︎
Disclosure: this work was partially funded by a grant from Mozilla, in a program operated by my department. ↩︎
In a real-world example, one might well prune out these common not-very-meaningful words. ↩︎
Note that you might use a different algorithm to compute the embeddings on the documents as on the queries, for instance if you are doing text search over images. For the purposes of this post, however, this is not important. ↩︎
Note that this is basically the same trick that PIR schemes use. ↩︎