How to securely vote for (or against) Elon Musk

Maybe Internet voting is a good idea just this one time...

Posted by ekr on 24 Dec 2022

Note: this post contains a bunch of LaTeX math notation rendered in MathJax, but it doesn't show up right in the newsletter version. You may want to instead read the version on the site.

Earlier this week Elon Musk ran a poll for whether he should step down as head of Twitter. As of this writing, the poll stood overwhelming (57.5 to 42.5) against Musk.

Should I step down as head of Twitter? I will abide by the results of this poll.

— Elon Musk (@elonmusk) December 18, 2022

Unsurprisingly, there have been claims of voter fraud (via "bots") as well as concerns that Musk would retaliate against people who voted that he should step down. Twitter polls are just some code on a Web site, and so are trivially insecure in any number of ways, including:

• There's no way to validate who voted.

• There's no way to externally verify that the votes were accurately counted.

• It's trivial for anyone in control of Twitter servers to see who voted which way.

These weaknesses follow directly from the way that Web sites are built: your browser is just running a program that is provided by the server, and you vote by sending your vote to the server, so of course the server can see your vote and lie about it. The typical way to address this is with physical countermeasures like having people vote with paper ballots or having some kind of paper trail of how people voted. However, over the past 25 years or so it's become possible to build a voting system that is entirely remote (i.e., that doesn't involve you voting in person or sending any physical object anywhere) and yet provides strong privacy and security guarantees [terms and conditions apply].

These technologies are typically called cryptographic or more recently end-to-end (E2E) voting systems. There has been an enormous amount of work in this area; in this post, I'll be describing a simplified version of a pair of papers by two of the pioneers of the field, Josh Benaloh and Ben Adida (Helios).

Background #

Before we get into end-to-end systems, it's useful to review how a typical paper ballot system works. You can find a more detailed description in previous posts and a description of the requirements here. Typically you have preprinted paper ballots which lists the choices for each contest. For instance:

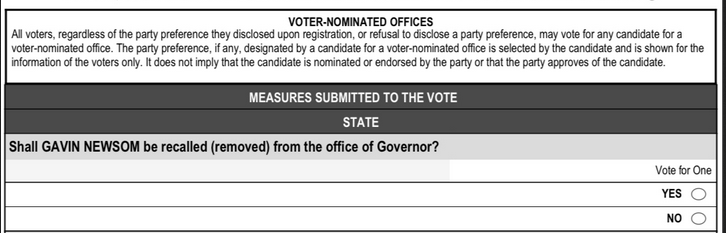
The voter marks the ballot with their selection and then submits it for tabulation. In many (though not all systems) the ballot is then mixed with other ballots and shuffled (or maybe at least shaken around a bit) so that the order in which people voted is not preserved. For instance, they might be put in a cardboard box, shuffled, and then carried to some central place for tabulation. The ballots are then tabulated and the totals reported.

This system has a fairly straightforward verifiability story if you can observe the process: you can observe who voted and that each voter only got a single ballot. As long as the chain of custody for ballots is secure (i.e., the ones that go into the box are the ones that are counted) and then can observe the counting process, then you can verify that the totals are right, and can have confidence in the whole election. The privacy story is similarly straightforward: the ballots are shuffled and as long as people don't mark them in a distinguishing fashion—a big assumption!—then it's not possible to associate a ballot with a given voter (what's called "k-anonymity").

How Not to Build a Cryptographic Voting System #

Building an end-to-end voting system is more or less a matter of replicating these properties without the paper. This is harder than it sounds. The basic problem is that there is a tension between two properties:

• Ensuring the integrity of the ballot through the entire process.

• Protecting the anonymity of individual votes.

If you're willing to give up either of these properties, then the problem becomes fairly straightforward.^[1]

Secure but Non-Anonymous Ballots #

If you're willing to sacrifice anonymity, then you can just have signed ballots. The way that this works is that each user has a cryptographic key pair (this of course imports all the usual problems with cryptographic identities, but let's assume that those are solved). In order to vote you sign your ballot and submit it to the election administrators.

The administrators post all the signed ballots on some public bulletin board. This allows anyone to verify who voted and file challenges^[2] in case of irregularities, such as:

• Their vote wasn't included
• Someone voted who shouldn't have
• Someone voted multiple times

Once the challenges are complete, everyone can then verify the tabulation for themselves. Of course, this also lets anyone know exactly how everyone else voted, which is bad.

Anonymous but Insecure Ballots #

On the other hand, if you don't care about the integrity of the election, you can use standard techniques to mix the ballots. For instance, you can have a series of proxies arranged in what's called a mix network (mixnet), as shown below:

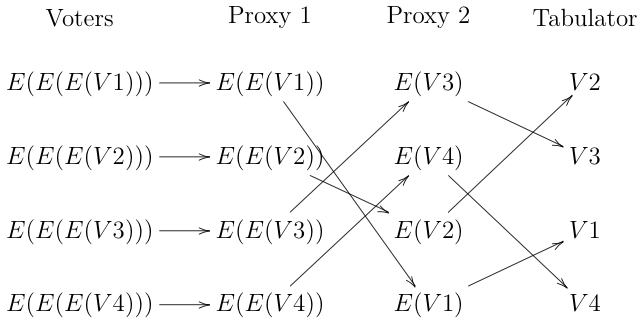
The idea here is that you have a series of independently operated proxies. Each voter recursively encrypts their ballot, first to the tabulator, then to proxy 1, and then to proxy 2. They then send their ballots to proxy 1, which decrypts them, shuffles them, and forwards them to proxy 2. Proxy 2 does the same and forwards them to the tabulator, which finally decrypts them. The end result is that the tabulator gets a list of ballots but is unable to determine which ballots correspond to which voter or what order they were cast in: it receives them in random order and because encryption was removed at each layer, there is no way to match the contents of a given ballot to the encrypted version that was cast. This property holds as long as at least one of the proxies is honest, and you can of course have an arbitrary number of proxies.

Unfortunately, any one of the proxies or the tabulator can tamper with the election results. It's obvious that the tabulator can do this because they have the final ballots, but the proxies can do the same by replacing the genuine ballots with fake ones. You could of course have the voters sign the ballots, but then this obviates the point of shuffling them because the voter's identity will be available to the tabulator. Even if you sign them before they are sent to the first proxy, that proxy has to strip the signatures.

Building a Real Design #

The underlying problem with the mixnet scheme is that it doesn't do anything to ensure that the ballots that come into the mixnet are the ballots that come out of it. In an ordinary paper-based system, this is provided by physical properties: you verify that the box is empty at the start of the election and you can have confidence that paper ballots won't change in transit or create new ballots via spontaneous generation. However, the proxies are much more complicated than cardboard boxes and they can readily create, modify, or delete ballots.

What we need is some way to verify the integrity of the mixing system, or more precisely, a way for a mixer to prove that it has executed the mixing correctly, which is to say that there is a one-to-one relationship between the ballots that were put into the system and those that came out. I describe how to build such a mixer below.

Re-Encryption #

In order to do this we first need a new primitive, which is a way to reencrypt a value encrypted to Alice so that the ciphertext (the encrypted value) is different but the plaintext (what you get when you decrypt) is the same. Importantly, you need to be able to do this without knowing the encryption key or the plaintext (it's trivial to do otherwise by just decrypting and reencrypting). In the simple proxy design above we just solved this problem by using nested encryption, but for reasons that will shortly become apparent, that doesn't work here, so we need a new primitive.

You can find details of how to implement reencryption here but we can just assume that we have some function $R$ that performs this operation. Specifically, given a ciphertext $C$ and a randomizer $r$, we can compute:

$$ R(r, C) \rightarrow C' $$

Such that:

$$ Decrypt(C) = Decrypt(C') $$

We can create a mixer by using re-encryption instead of removing one layer of encryption, as shown below:

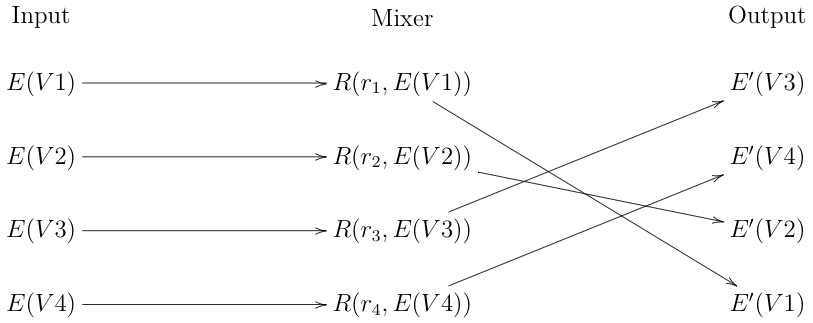
Without knowing the $r_i$ randomization values, it's not possible to associate the output ciphertexts with their corresponding inputs.

Unlike nested encryption, re-encryption has the nice property that you can re-encrypt the same ciphertext multiple times without any help from the sender. So, for instance, you can just add another mixer stage without having to add another layer of nesting. More importantly, you can can create an arbitrary number of equivalent ciphertexts from the same initial ciphertext. We use this fact below.

Provable Mixing #

Re-encryption-based mixing is a more flexible design than nested encryption, but this still leaves us trusting the mixer. However, once we base our mix on re-encryption we can prove that the mix was performed correctly.

It's of course trivial to prove that the mix was performed correctly if you're willing to reveal the mapping itself: you just publish which inputs correspond to to which outputs as well as the reencryption factors $r_i$ and anyone can verify for themselves that the ostensible inputs result in the right outputs. What we want to do however is prove that the mix was performed correctly without revealing the mapping between inputs and outputs, which is obviously harder. Fortunately, there is a clever trick we can use here, due to Sako and Kilian.

The basic idea is that instead of mixing the ballots once, the mixer instead does so twice, creating two alternative mixes. It publishes both of them, identifying (arbitrarily) one as the output and the other as what's called the "shadow" mix. The diagram below shows the situation, with dashed arrows to indicate that observers are unable to see the mapping:

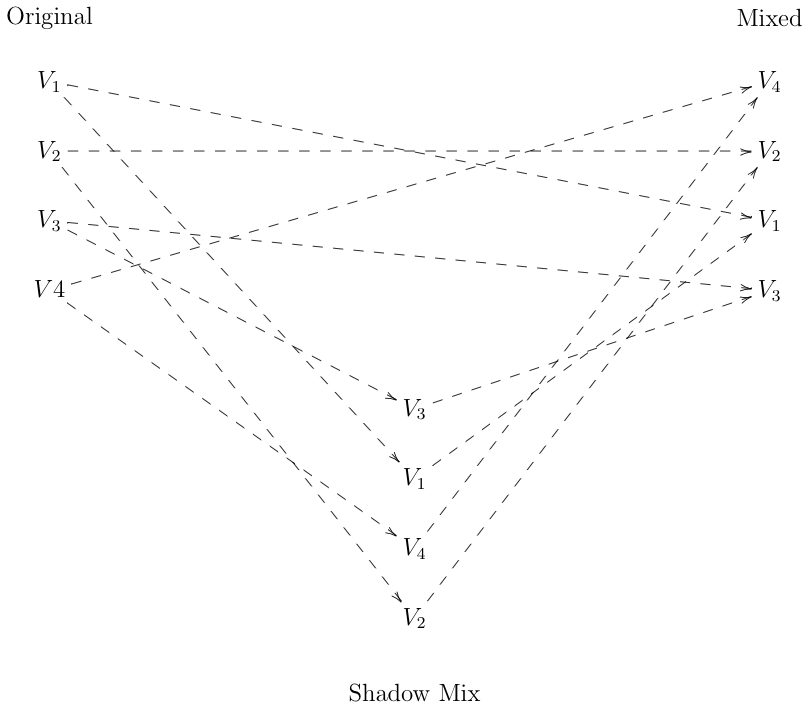
Now consider the case where the mixer cheated and replaced value $V_1$ in the output with a new value $V_a$. Assuming everything else was correct, the shadow mix can be in one of two states. First, the shadow mix can be correct, which is to say that it contains $V_1$ rather than $V_a$. In this case, there is a 1-1 mapping between the input values and the shadow mix, but no 1-1 mapping between the shadow mix and the outputs.

Alternatively, the shadow mix can be incorrect and contain $V_a$ rather than $V_1$. In this case, there is a 1-1 mapping between the shadow mix and the outputs but not between the shadow mix and the inputs.

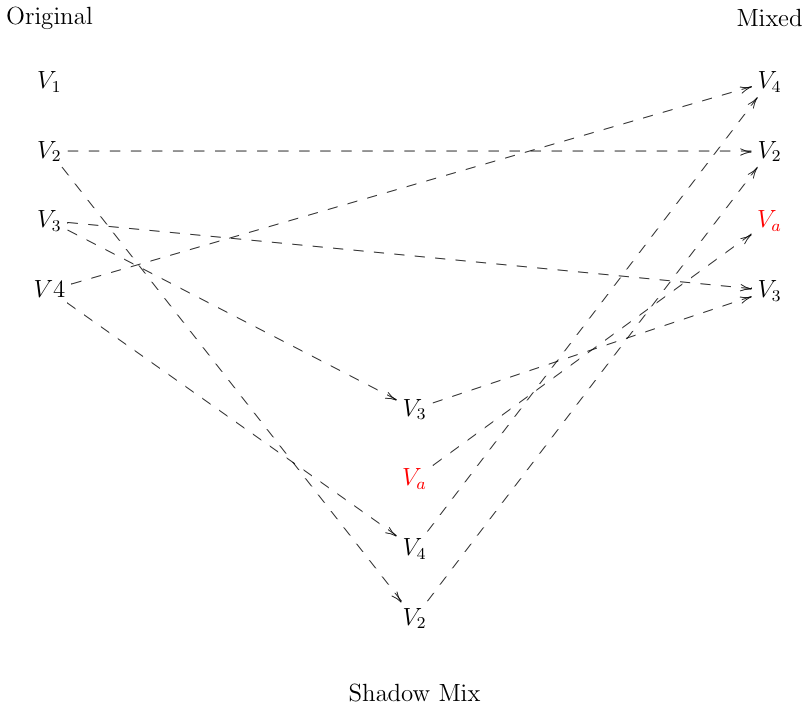
Either way, if the mixer cheated, there will either not be a mapping from the input to the shadow or from the shadow to the output (of course, it's possible for both to be wrong). If the verifier then randomly challenges the mixer to reveal either of the mappings, there is a $1/2$ chance that the mixer will be unable to do so (obviously, if the mixer discloses both, then this is the same as disclosing the full mapping to the output, but because the shadow mix is shuffled with respect to the input-output mappings, neither of the mappings to the shadow mix tells you anything about the input-output mappings). On the other hand, if the mixer has behaved honestly, it can reveal either mapping when challenged.

Given this design, if the mixer cheats they have a $1/2$ chance of getting caught, or, to look at it another way, a $1/2$ chance of getting away with it. It's straightforward, however, to make that chance arbitrarily small, just by having the mixer create more than one shadow mix. The verifier then asks them to reveal one half of the mapping for each of the shadows—but never both halves for a given shadow. Each of these challenges has a $1/2$ chance of detection, so if you have $n$ challenges, the chance of successful cheating is $2^{-n}$, which quickly gets very small; somewhere between 80 and 100 shadows is easily sufficient.

Note that this does not prove that the ballots were actually randomly^[3] shuffled, merely that they map 1:1 between input and output. The standard way to ensure shuffling is to have multiple mixers: as long as any one is honest and actually shuffles, the result will be random.

A non-interactive proof #

The obvious problem here is that this proof of correctness is interactive which is to say that it requires someone to actually generate the challenges. If you're not that person you just have to trust them. This is still better than nothing because the verifier could be separate from the mixer, but it's possible to do better still, creating a non-interactive proof that the mix was done correctly.

The intuition to have here is that the interactive proof works by forcing the mixer to commit to the outputs before they get to learn the challenge. This prevents the mixer from creating a specific dishonest mapping that will pass a specific known challenge, which is quite easy (just make the challenged side correct). However, we can achieve the same effect by making it impossible for the dishonest mixer to control the challenge for a given set of mappings. We do this by computing the challenge using a hash of the outputs. I.e., the mixer:

1. Computes the output and $n$ shadow mixes $S_1, S_2, ... S_n$.
2. Hashes those to produce a string of at least $n$ bits ($H_i$)
3. Publish the output and shadow mixes and also for each bit of the hash $H_i$, publish either the mapping from the input to the shadow (if the bit is 0) or from the shadow to the output (if the bit is 0).

The verifier then recomputes the hash over the outputs and checks that the mixer has provided valid mappings for the indicated side.

It's natural to wonder whether the mixer could compute a mapping such that the hash has the right set of challenges. In principle yes, but because the hash is an unpredictable function of the mappings, they have to first compute the mapping and then check whether it works. You have a random $2^{-n}$ chance of getting a matching mapping, and so you just have to keep trying; it costs about $2^{n/2}$ operations to find an appropriate input, which is prohibitive if $n$ is large enough.

The problem of turning an interactive proof into a non-interactive one occurs all over cryptography, and this hashing technique, called the Fiat-Shamir Heuristic, is the standard solution.

Tabulation #

Once we have a shuffled set of encrypted ballots, we need to count them. At a high level, this is simple: the election officials decrypt them to reveal the original ballots. They publish those ballots and anyone can then tabulate them themselves. However, there are two subtleties we need to consider here.

Verifiable Decryption #

The first problem we have is that the election officials could simply lie about the contents of the ballots. I.e., they could say that a vote for Alice was actually a vote for Bob. This actually turns out to have an easy answer: it's possible for them to create a proof that they correctly decrypted the ballot. The details are a bit complicated but don't really matter: the bottom line is that it's possible to publish the following triplet:

• The encrypted ballot $E(V_i)$
• The decrypted ballot $V_i$
• A proof that $E(V_i)$ decrypts to $V_i$.

Once verifiers have checked that the proofs are correct, they can then tabulate the decrypted ballots.

Multiple Decryption Keys #

The second problem is that election officials might decrypt the encrypted ballots when they are initially posted on the bulletin board, this learning how everyone voted. As noted above, these ballots are signed and so are easy to attribute.

The standard approach to mitigating this threat is to encrypt each vote with multiple keys, so that you need multiple election officials—or even some trusted third party—to do the decryption. This means that they all need to collude in order to violate user privacy by decrypting ballots before they are shuffled. This is cryptographically straightforward (see here for one way to do it with ElGamal Encryption). Note that even if election officials do all collude, this still doesn't threaten the integrity of the election.

Putting it all Together #

We now have the makings of a complete system, shown in the figure below:

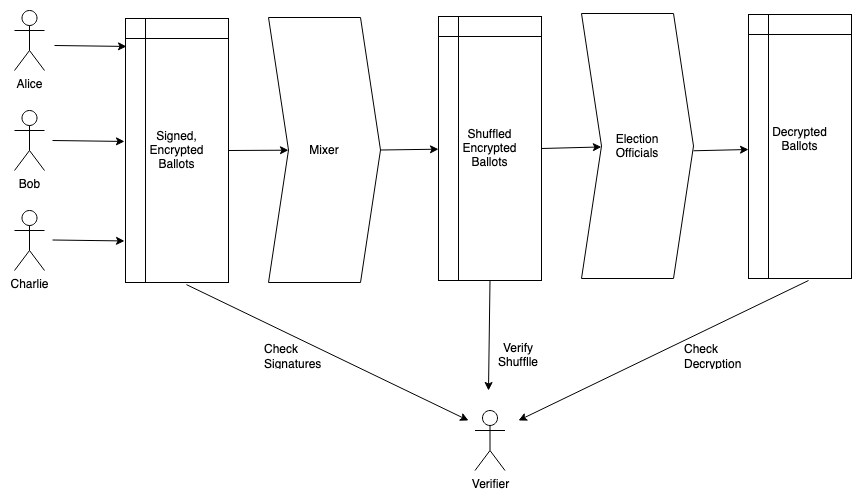
The election process looks like this:

1. To cast their ballot, each voter encrypts it with the public key(s) of the election officials and then signs it with their own private key. They post it to the bulletin board.

2. Once the ballots are all cast, the mixer strips the digital signatures (thus anonymizing them), shuffles the ballots, and posts them along with the proof of correct shuffling to the bulletin board. This can be the same bulletin board or a separate one.

3. The election officials take the shuffled ballots, decrypt them, and posts the decrypted ballots along with their proofs of correct decryption.

In order to verify the election, you take the following steps:

1. Check the signatures on the ballots. This ensures that the right set of voters cast their votes and that they attest to the contents.

2. Check the proof of shuffling. This ensures that the the shuffled ballots correspond to the ballots you verified the signatures on (though you can't tell which ones are which).

3. Check the proof of decryption. This ensures that the plaintext ballots correctly match the encrypted ballots.

Any observer can take these steps without any help from the voting officials.

If all the steps complete successfully, you have then verified that the output decrypted ballots have a 1:1 relationship with the signed ballots that you verified and hence with the ballots you expected to be cast, and therefore that the election was conducted correctly. You can then tabulate the ballots in the usual way and verify that the totals match what you expected, thus verifying the entire election.

Against Internet voting #

E2E voting is an amazing technical achievement, but despite that, the broad consensus of people working in voting is that Internet voting is a bad idea, even using E2E systems. Why the incongruity? The reason is that voting isn't just a technology, but rather is embedded in a whole election system, and it's in that context that E2E voting falls short.

Voting Device Security #

The first problem is that unlike (say) hand-marked paper ballots, cryptographic voting systems require users to vote on some sort of computer (you weren't planning to do elliptic curve math in your head, right?). There are two main ways for this to work:

1. You can use the same types of electronic polling place devices that people use for voting now.

2. You can vote on your own device (e.g., your phone).

But this means that you're trusting that computer to actually correctly cast your votes and computers are incredibly hard to secure, as we've seen this repeatedly in the elections context, where third party audits have repeatedly shown that even temporary access to polling place voting devices is sufficient to subvert them (see, for instance the reports from the California Top-to-Bottom Review back in 2007). The situation isn't much better with personal devices, which need regular updating to address a constant stream of discovered vulnerabilities (just as an example, here's the list of security issues in the latest iOS release; any major system has a similar list).

There has been some good work on allowing users to verify that their votes were correctly (see for instance Section 4 of Benaloh06). This is a more complicated problem than it seems because it's important to avoid providing the voter with a receipt that could be used to prove how they voted (as opposed to that they voted). Otherwise, this receipt can potentially be used to enable vote buying. Of course, these approaches ultimately require the voter to use some other computer to verify whatever proof the voting device spits out.

Even with these systems, you are left with roughly the same situation as with a Ballot Marking Devices (BMDs): users can in principle verify their votes but often do not. Specifically, suppose a machine is programmed to change 1/100 votes from Smith to a vote for Jones by acting as if the user had pressed the wrong button (ever make a typo on your phone?). If a user does verify their vote, the attack succeeds, and if the user does check, the machine allows them to correct it. Because users can and do accidentally vote for the wrong person, this type of attack is very hard to distinguish from voter error. Studies of Ballot Marking Devices (BMDs) by Bernhard et al. found that if left to themselves around 6.5% of voters (in a simulated but realistic setting) will detect ballots being changed. There is some good news here, which is that with appropriate warnings by the "poll workers" the researchers were able to raise the detection rate to 85.7%, though it's not clear how feasible it is to get poll workers to give those warnings. Given that checking a paper ballot is much easier than checking a cryptographic ballot, we should expect a fairly low rate of checking.

I do want to note that we are starting to see some interest in adding E2E to paper-based election systems, as in STAR-Vote or with Microsoft's ElectionGuard. This seems like a potentially good idea in that it augments the security of the paper-based system. However, in systems with no paper trail, such as voting from user's phones, then we're left just depending on the security of the device itself. The threat to be most concerned about here is an attack that compromises a large number of voter's devices, and through them the integrity of the election. Even if you subsequently managed to gather evidence that this had happened on a large scale, figuring out what to do after would be a political nightmare.

Operational Challenges #

Even if we assume that the voting devices are uncompromised, the actual logistics of building an operational E2E system are extremely challenging. Elections themselves are complicated to run—if you want to get a real sense of this, I recommend serving as a poll worker—and there are a lot of things that can go wrong; adding a bunch of complicated critical-path technology creates a lot of new opportunities for failure.

Server Infrastructure #

For example, if you want to have an Internet voting system you need some servers which accept the votes. What happens if those servers go down on election night or—worse yet—are attacked? These protocols are designed to be resistant to misbehavior by the voting servers in the sense that they can't tamper with the results, but this doesn't address attacks designed to prevent users from voting. Typical paper-based elections have mechanisms for addressing this kind of failure: if the voting machines fail, you can fall back to paper; if the electronic poll books fail, you may have paper records; if those paper records are unavailable, people can file provisional ballots and you can sort it out later. However, these mechanisms all depend on people already being in the polling place; if they're at home and things fail, the election can completely fail.

It's also possible to selectively mount attacks, for instance by having a compromised server reject only certain people's votes or by mounting a denial-of-service attack on certain precincts; this is a particularly powerful form of attack in the United States, where voting is managed locally, and so you could attack the infrastructure of a county that leans to one political party but ignore the infrastructure of a county that leans the other way.

Client Infrastructure #

As discussed above, in order to successfully vote on the Internet, the voting software needs to run on a device controlled by the voter. Even if we ignore attack, this is a prime opportunity for things to go wrong: here we have a piece of software which needs to be developed at low cost, run on more or less every device that anyone might have, needs to operate essentially perfectly, and only gets used once of twice a year. This is a tall order for any software shop.

To make matters worse, we have the problem of voter authentication. For obvious reasons, we need each voter to prove that they are authorized to vote, which means giving them some kind of credential. There are a lot of options here (give them a digital certificate, mail them a code, etc.) but whatever you do, they are all subject to voters losing their credentials. In ordinary Website authentication, we usually allow users to reset their passwords via e-mail or SMS, but for obvious reasons that's not OK here (allowing Gmail and T-Mobile to have the ability to impersonate a huge fraction of voters really undercuts the value of E2E voting). Here too, we're stuck with a situation where the failure happens at the worst possible time, and recovery entails actually going somewhere.

Implementation Complexity #

Next, we have to contend with the problem of implementation complexity. Even the best E2E voting systems are fairly complex, and the systems they need to be embedded in are even more complex. This means that even if we have a system design which is secure, we still have to worry about implementation errors, both of the protocol itself and of the rest of the infrastructure. So far, there hasn't been that much Internet voting, but serious errors have been found in several early systems. See for instance, the analysis of the Scytl system by Haines, Lewis, Pereira, and Teague^[5] and of the Voatz mobile voting system by Trail of Bits, so the situation is not encouraging.

Voter Comprehension #

Finally, we have the problem of voter understanding. It's not enough for the election just to produce the right result, it must also do so in a verifiable fashion. As voting researcher Dan Wallach is fond of saying, the purpose of elections is to convince the loser that they actually lost. With paper-based ballots, the chain of reasoning for how the election was decided is relatively straightforward: ballots go into the box and you count them. Despite this, we've still seen extensive attempts to question the resulting count, as in the 2020 US Presidential Election.

By contrast, the security of E2E voting depends on some fairly complicated cryptography that practically nobody understands. I've just spent 4000-odd words on this topic and it's only that short because I didn't explain how any of the actual cryptographic pieces work and just focused on the system logic; if you want to convince yourself that ballots were cast correctly you have to not just have a surface understanding of the cryptography but also have confidence that the mathematical problems it's based on are really hard. We don't even know for sure that that's true in the classical setting and we know that they're not if someone ever builds a big enough quantum computer. Try explaining that to your average voter.

Final Thoughts #

My point here is not to criticize E2E voting, which is an amazingly cool technology. The problem is that it's necessary but not sufficient for Internet voting, which requires correct operation of systems which are not covered by the cryptography, all under very challenging conditions. However, E2E does have two important use cases: first, it's potentially useful as an additional measure of security for in-person paper-based systems, such as Ballot Marking Devices. Second, there are lots of low to medium-stakes situations where people are already voting over the Internet using systems which are tragically insecure. These elections would be much safer and more private if they used E2E systems, even if those systems were still imperfect. So when do we get our E2E secure Twitter polls?